Paradoxe du carré manquant
En géométrie, le paradoxe du carré manquant est une apparente démonstration géométrique d'un résultat impossible, reposant sur une illusion d'optique.
Le paradoxe, et son explication
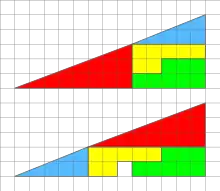
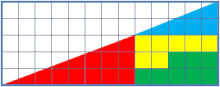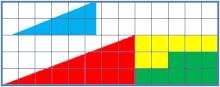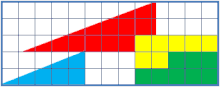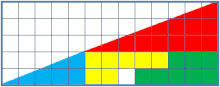
Si on découpe un triangle selon un quadrillage, de telle sorte que plusieurs reconstructions du triangle soient possibles, alors il y a certaines constructions où il manque un carré unitaire. C'est en effet très étonnant, car l'aire du triangle peut être décomposée : c'est la somme des carrés qui le composent — par extension la somme des carrés qui composent les formes de base.
Dans notre exemple, on décompose un triangle rectangle dont la longueur de la base et de la hauteur valent respectivement 13 et 5, en quatre régions :
- Vert : 8 carrés
- Jaune : 7 carrés
- Bleu : 5 carrés
- Rouge : 12 carrés
Cela donne un triangle d'aire 12 + 5 + 7 + 8 = 32. Or si on applique la formule de l'aire au triangle, on obtient 13 × 5 / 2 = 65/2 = 32,5.
Finalement, la « surface manquante » ne fait que compenser l'écart entre la légère convexité et la légère concavité des fausses hypoténuses des prétendus triangles. Le triangle bleu et le triangle rouge n'ayant pas la même pente, la prétendue hypoténuse de la première figure est concave, tandis que l'autre est convexe.
Cette construction géométrique est liée à la suite de Fibonacci. En effet, la différence entre le produit de deux termes consécutifs de cette suite (ici 3 et 5) et le produit des deux termes adjacents (ici 2 et 8) vaut toujours 1. On peut donc réaliser sur le même principe de faux triangles de côtés 2 et 5, 3 et 8, 5 et 13 (comme ici), 8 et 21, etc.
Autres constructions analogues
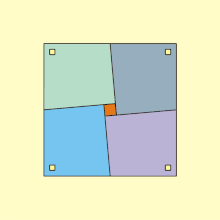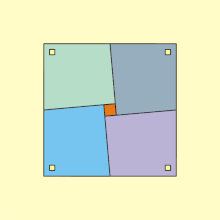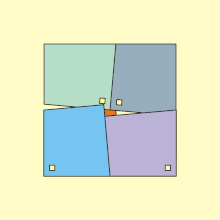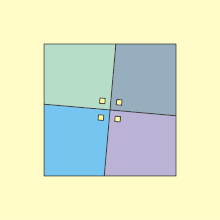
Une variante de cette idée, montrée dans l'animation à gauche, utilise quatre quadrilatères et un petit carré ; quand on fait pivoter les quadrilatères, ils comblent le carré central, bien que l'aire totale de la figure semble inchangée. Ce paradoxe apparent s'explique par le fait que le côté du nouveau carré est en fait un peu plus petit que celui du carré initial. Si θ est l'angle entre les côtés opposés des quadrilatères, alors le rapport des deux aires est donné par sec2θ – 1. Pour θ = 5°, il vaut 1,00765, ce qui correspond à une différence d'environ 0,4 % entre les côtés des deux grands carrés.
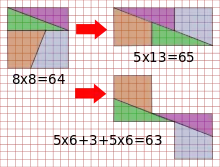
La décomposition de droite, transformant un carré d'aire 64 en un rectangle d'aire 65, est due à Sam Loyd[1] ; ici, l'explication du paradoxe vient de ce que les côtés des pièces ne s'identifient pas tout à fait, laissant vide un mince parallélogramme d'aire unité au centre du rectangle.
Toutes ces « démonstrations » de résultats absurdes peuvent aussi être vues comme une incitation à se méfier des preuves sans mots, des figures approximatives [2], des jeux dans les dispositifs correspondants, et à ne pas s'en contenter sans se convaincre qu'elles peuvent être rendues rigoureuses[3].
Notes
- Ou plutôt à son fils, d'après Martin Gardner ; elle pourrait cependant être antérieure ; voir Sam Loyd's son's dissection (en).
- « La géométrie est l'art de raisonner juste sur des figures fausses », disait cependant Descartes.
- Claudi Alsina et Roger B. Nelsen, « An Invitation to Proofs Without Words »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (en).
Voir aussi
Liens externes
- (en) Curry's Paradox: How Is It Possible? sur cut-the-knot
- (en) Magic Triangles, or the Area Paradox par Gianni A. Sarcone sur archimedes-lab.org (en)