Mutation (théorie des nœuds)
En théorie des nœuds, une mutation est une opération transformant un nœud en un nœud ayant le même nombre de croisements.
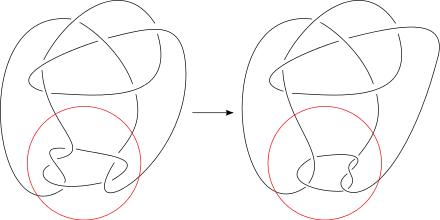
Soit K un nœud donné par son diagramme, et considérons dans le plan du diagramme un disque tel que sa circonférence coupe K exactement quatre fois. On peut supposer (à isotopie du plan près) que ce disque est géométriquement rond et que les 4 points d'intersection sont régulièrement espacés sur le cercle. Il y existe deux réflexions conservant globalement le disque ainsi que ces 4 points, ainsi que la rotation composée de ces deux réflexions. Une mutation consiste à effectuer l'une de ces 3 transformations à l'intérieur du disque, et le nouveau nœud obtenu est appelé un mutant de K. Deux nœuds obtenus l'un de l'autre par mutation forment une paire de nœuds mutants.
Deux nœuds mutants ont en général beaucoup d'invariants identiques (en particulier le même volume hyperbolique (en) (résultat de Daniel Ruberman), et le même polynôme HOMFLY (en)) mais ils peuvent être non isomorphes.
Exemples
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Mutation (knot theory) » (voir la liste des auteurs).
- (en) Colin Adams (en), The Knot Book, AMS, , 320 p. (ISBN 978-0-8050-7380-5 et 0-8050-7380-9)