Modélisation mathématique d'un labyrinthe
Les labyrinthes peuvent être étudiés comme des objets mathématiques, c'est la modélisation mathématique de labyrinthe. Deux aspects importants de cette modélisation sont la génération automatique de labyrinthe et la résolution de labyrinthe.
Classification des labyrinthes
Un labyrinthe est une surface connexe. De telles surfaces peuvent avoir des topologies différentes : simple, ou comportant des anneaux ou îlots[1]:
 |
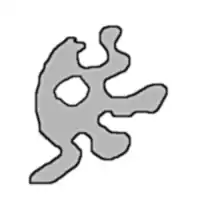 |
Ces deux surfaces ne sont topologiquement pas équivalentes. Cette différence, rapportée aux labyrinthes, conduit à une distinction en deux catégories :
- celle des labyrinthes dits « parfaits » où chaque cellule est reliée à toutes les autres et, ce, de manière unique[2].
- celle des labyrinthes dits « imparfaits » qui sont tous les labyrinthes qui ne sont pas parfaits (ils peuvent donc contenir des boucles, des îlots ou des cellules inaccessibles).
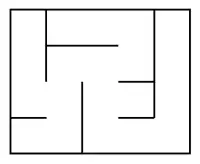 |
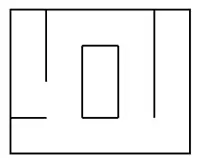 | |
| Labyrinthe « parfait » | Labyrinthe « imparfait » | |
Notion de chemin dans un labyrinthe
Les chemins des labyrinthes parfaits peuvent être représentés par des graphes orientés acycliques (ou DAG pour directed acyclic graph) :
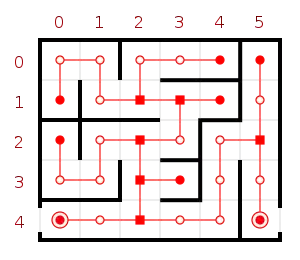 Un labyrinthe parfait et son DAG associé (en rouge). Les nœuds sont marqués selon qu'il s'agit d'entrées ou de sorties, d'intersections ou de cul-de-sac. |
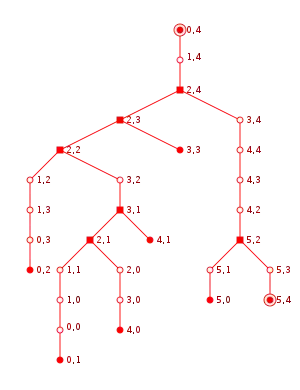 Représentation en arbre du labyrinthe |
Résolution
La résolution de labyrinthe consiste à trouver la sortie d'un labyrinthe modélisé mathématiquement. Il existe plusieurs algorithmes pour ce problème.
Génération
Les algorithmes proposés ici vont s'intéresser aux labyrinthes parfaits, mais quelques adaptations permettent de créer facilement des labyrinthes à îlots. Ils sont basés sur l'espace discrétisé dont les cellules carrées sont initialement remplies et séparées par des cloisons, selon les quatre directions (nord, sud, est et ouest).
Un labyrinthe rectangulaire parfait de colonnes par lignes est un ensemble de cellules reliées les unes aux autres par un chemin unique. L'équivalence topologique des surfaces connexes simples va nous servir pour affiner notre vision des labyrinthes parfaits :
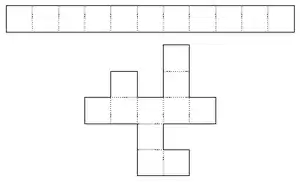
Le nombre de murs ouverts pour permettre un chemin unique dans un labyrinthe de cellules est identique au nombre de murs ouverts pour un chemin droit de cellules, soit murs.
Dans un rectangle cellules, le nombre total de murs internes possible est : . Pour obtenir ce résultat, on compte deux murs par cellule, par exemple celui du bas et celui de droite (on évite ainsi de recompter deux fois les mêmes) et on retire le nombre de murs limitant le rectangle en bas et à droite .

Le nombre de murs fermés dans un labyrinthe parfait est donc :
Algorithmes de construction de labyrinthes
Il existe de nombreux algorithmes de construction de labyrinthes. Voici deux d'entre eux assez simples.
Fusion aléatoire de chemins

Cet algorithme utilise une propriété des labyrinthes parfaits précédemment énoncée telle quelle : Chaque cellule est reliée à toutes les autres, et ce, de manière unique. Il fonctionne en fusionnant progressivement des chemins depuis la simple cellule jusqu'à l'obtention d'un chemin unique[3], il suit donc une approche ascendante.
L'algorithme associe une valeur unique à chaque cellule (leur numéro de séquence, par exemple) et part d'un labyrinthe où tous les murs sont fermés.
À chaque itération, on choisit un mur à ouvrir de manière aléatoire.
Lorsqu'un mur est ouvert entre deux cellules adjacentes, les deux cellules sont liées entre elles et forment un chemin.
À chaque fois que l'on tente d'ouvrir un mur entre deux cellules, on vérifie que ces deux cellules ont des identifiants différents.
- Si les identifiants sont identiques, c'est que les deux cellules sont déjà reliées et appartiennent donc au même chemin. On ne peut donc pas ouvrir le mur.
- Si les identifiants sont différents, le mur est ouvert, et l'identifiant de la première cellule est affecté à toutes les cellules du second chemin.
Finalement, on obtient un chemin unique lorsque le nombre de murs ouverts atteint , ce qui donne 19 étapes dans l'exemple ci-contre.
Pour l'affectation des identifiants aux cellules, une variante plus efficace serait d'employer des structures d'Union-Find, qui permettent de diminuer la complexité algorithmique de cette opération.
Différentes structures de données sont envisageables pour la représentation du labyrinthe dans un programme.
La plus simple consiste à définir deux matrices de valeurs booléennes, l'une de taille (m+1) x n qui va définir l'existence des murs verticaux entre les différentes cases de la grille, l'autre de taille m x (n+1) qui va représenter les murs horizontaux de manière similaire. Cette structure de données est alors adaptée au tracé de la grille.
Exploration exhaustive

On part d'un labyrinthe où tous les murs sont fermés. Chaque cellule contient une variable booléenne qui indique si la cellule a déjà été visitée ou non (i.e. les cellules visitées sont celles qui appartiennent au chemin du labyrinthe en cours de construction).
Au départ, toutes les cellules sont marquées comme non visitées (faux).
On choisit arbitrairement une cellule, on stocke la position en cours et on la marque comme visitée (vrai).
Puis on regarde quelles sont les cellules voisines possibles et non visitées.
S'il y a au moins une possibilité, on en choisit une au hasard, on ouvre le mur et on recommence avec la nouvelle cellule.
S'il n'y en pas, on revient à la case précédente et on recommence.
Lorsque l'on est revenu à la case de départ et qu'il n'y a plus de possibilités, le labyrinthe est terminé.
L'historique des emplacements des cellules précédentes peut être géré de deux façons équivalentes :
- par la sauvegarde dans un tableau de
- par la sauvegarde dans la pile, en utilisant la récursivité
La formulation récursive donne de très bons résultats pour des labyrinthes de taille modeste. Dès lors que l'on veut générer de grands labyrinthes (1000 x 1000, par exemple), le programme risque de se terminer brutalement si la taille de la pile est insuffisante. Il est donc important de prévoir une taille de pile suffisante ou à défaut de passer à une autre solution comme l'historique à base de tableau.
L'exploration exhaustive est moins complexe que la fusion de chemins car elle ne nécessite pas la mise en œuvre de structures complexes[4].
Discussion
Les deux types d'algorithmes ne sont pas tout à fait équivalents d'un point de vue qualitatif.
Le premier type fournit un labyrinthe dont l'arbre est statistiquement mieux équilibré (ou balancé) que celui généré par le second.
En effet, tous les murs ouvrables ont statistiquement approximativement autant de chances d'être ouverts.
Le premier algorithme favorisera l'apparition des bifurcations.
A contrario, le second privilégie les chemins. Les arbres seront donc assez fortement déséquilibrés. Plus un chemin est généré tôt, et plus il a de chances d'être long. Plus il est généré tardivement et plus il a de chances d'être court.
Le labyrinthe final sera composé de quelques chemins assez longs avec peu de ramifications et les ramifications auront une taille moyenne très inférieure au chemin sur laquelle elles se greffent.
Pour des labyrinthes de petite taille, les deux algorithmes donneront des résultats comparables. En revanche, les grands labyrinthes auront des apparences dissemblables.
D'un point de vue quantitatif, le second type d'algorithme sera en moyenne plus rapide que le premier. Une fois encore, sur de petites surfaces, les temps seront comparables. Mais sur de grandes surfaces, le second se montrera plus performant.
Du point de vue de la mise en œuvre, les deux algorithmes présentés sont probabilistes et à horizon fini, car le nombre de murs à enlever aléatoirement est connu. En revanche, alors que le premier nécessite une gestion lourde de l'ensemble des murs à considérer, le second est plus simple par sa gestion de l'historique des cellules visitées.
Notes et références
- Jérôme Cottanceau, Le choix du meilleur urinoir : Et 19 autres problèmes amusants qui prouvent que les maths servent à quelque chose !, Paris, Belin, coll. « Science à plumes », , 216 p. (ISBN 978-2-7011-9766-1), chap. 18 (« À quoi servent les maths... À ne pas rester piéger dans un labyrinthe ? »).
- « Labyrinthes », sur ilay.org (consulté le )
- (en) « Buckblog: Maze Generation: Kruskal's Algorithm », sur weblog.jamisbuck.org (consulté le )
- (en) « Buckblog: Maze Generation: Recursive Backtracking », sur weblog.jamisbuck.org (consulté le )
Liens externes
- Yann Langlais, Algorithmique pratique et optimisation de code : La génération de labyrinthes
- (en) Think Labyrinth: Maze algorithms (explications détaillées sur les algorithmes de génération de labyrinthe)
- Jamis Buck, « Maze Algorithms (visualisation de différents algorithmes de génération de labyrinthes) »
Bibliographie
- Jérôme Cottanceau, Le choix du meilleur urinoir : Et 19 autres problèmes amusants qui prouvent que les maths servent à quelque chose !, Paris, Belin, coll. « Science à plumes », , 216 p. (ISBN 978-2-7011-9766-1), chap. 18 (« À quoi servent les maths... À ne pas rester piéger dans un labyrinthe ? »).






