Modèle astronomique pythagoricien
Le modèle astronomique pythagoricien est un ancien système astronomique, dont le développement est attribué à Philolaos de Crotone.
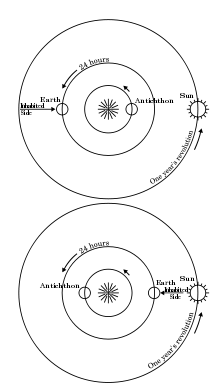
Description
Ce modèle n'est ni géocentrique ni héliocentrique. Il décrit la Terre et le Soleil, tournant tous deux autour d'un même foyer central, hypothétique. La Terre est une sphère et présente toujours la même face, inhabitée, au foyer central. Son orbite dure 24 heures tandis que le Soleil suit une orbite beaucoup plus grande, sur une année. Quant à la Lune, elle orbite aussi autour du feu central, suivant une orbite plus vaste que celle de la Terre, mais plus petite que celle du Soleil[1].
Le modèle prévoit l'existence d'une Anti-Terre, qui serait toujours en opposition avec la Terre et serait par conséquent invisible.
Attribution et historique
Ce modèle est attribué par Aristote à l'école pythagoricienne. Aucune donnée plus précise ne permet de l'attribuer ; il n'existe pas de traces d'éventuels travaux de Pythagore lui-même sur l'astronomie. Sans plus de précision, il reste donc attribué à cette école, ce qui ne signifie aucunement qu'il était admis par l'unanimité de ses membres. L'attribution à Philolas s'appuie sur des fragments de documents dont l'authenticité est douteuse[2].
Les raisonnements qui ont mené à concevoir ce modèle semblent plus mystiques qu'astronomiques : ainsi l'existence d'un feu central est jugée nécessaire car le feu, le plus précieux des quatre éléments, doit occuper une position d'honneur. Cependant, il était précurseur par certains aspects : il était notamment le premier à attribuer une orbite à la Terre[3].
Notes et références
- Hypothèses astronomiques de Pythagore et de Philolaus, Martin (Thomas Henri)Thomas Henri MartinJan 1872
- Joseph Moreau, « L'essor de l'astronomie scientifique chez les Grecs », Revue d'histoire des sciences, vol. 29, no 3, , p. 193–212 (DOI 10.3406/rhs.1976.1407, lire en ligne, consulté le )
- Guy Donnay, « Le système astronomique de Platon », Revue belge de philologie et d'histoire, vol. 38, no 1, , p. 5–29 (ISSN 0035-0818, DOI 10.3406/rbph.1960.2304, lire en ligne, consulté le )