Ludion (physique)
Le ludion est un montage de physique (ou un jouet) illustrant la forte compressibilité de l'air (par rapport à l'eau, très peu compressible) : un objet creux et rempli d'air est immergé dans un récipient fermé par une membrane. L'air qu'il contient sert à le faire flotter. L'apparition d'une pression sur la membrane fait descendre l'objet creux et l'arrêt de la pression le fait remonter.
.jpg.webp)
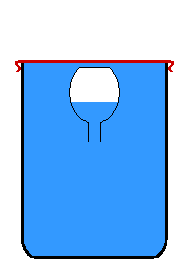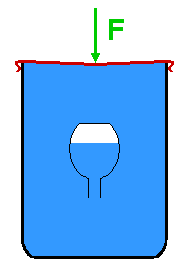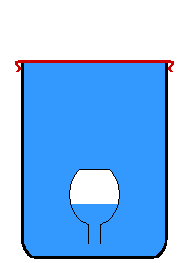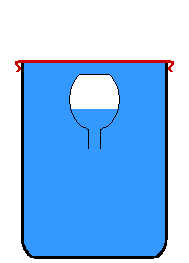
Intervient en premier lieu la transmission de la pression par le liquide : celui-ci ne pouvant en première approximation pas être comprimé[1], il transmet la pression à l'air se trouvant dans l'objet creux. L'air se comprime et son volume diminue. Cet air prend alors moins de place. La place libérée par l'air est alors occupée par le liquide. L'objet descend donc car la poussée d'Archimède qu'il subit diminue par la perte de volume de la bulle d'air qui le fait flotter. Le ludion coule car son accélération prend alors les mêmes directions et sens que ceux de la nouvelle résultante des forces appliquées en son centre de gravité.
C'est le principe du ballast des sous-marins.
Ce principe permet aussi de montrer la diminution du volume d'air avec l'augmentation de la profondeur lorsque l'on pratique la plongée sous-marine : plus l'on descend, plus le plongeur consomme une grande quantité d'air à chaque inspiration, puisqu'à volume constant (V1=V2), la quantité d'air contenue dans les poumons augmente avec la profondeur selon la loi de Mariotte : P1×V1 = P2×V2, P étant la pression, V le volume, 1 l'état initial et 2 l'état final.
De même, un ballon gonflé a un volume plus important à la surface de l'eau qu'au fond. Remarquons que la sensibilité du ludion à la pression est trop faible pour en faire un baromètre, devant les autres paramètres (solubilité de l'air dans l'eau, température…).
Construire un ludion
Matériel
- Une bouteille en plastique (soda, 1,5 litre)
- Un tube de stylo à bille
- Un ou plusieurs trombones
- Du ruban adhésif transparent
- Des ciseaux
Construction
Commencer par boucher, à l’aide d’un morceau de ruban adhésif, le petit orifice présent au milieu du stylo. Accrocher ensuite le trombone à la partie intérieure du tube (du côté de l’ouverture). Une fois la bouteille remplie d’eau, enlever le petit bouchon du stylo, tremper le tube aux trois quarts dans la bouteille et rebouchez : le tube est rempli d’eau aux trois quarts. Placer enfin le tube dans la bouteille ; celui-ci doit flotter verticalement. Reboucher la bouteille.
Test
Il suffit d’appuyer sur la bouteille pour faire descendre l'objet. En effet, lorsque l'on appuie sur la bouteille, la pression augmente à l'intérieur. Seul l'air étant compressible, l'air contenu dans le corps du stylo est donc comprimé, et son volume décroit. La poussée d'Archimède décroit d'autant et le stylo coule.
Explication
Bien souvent en physique, il est utile de faire un schéma regroupant toutes les informations connues afin de déterminer l’ensemble des paramètres expérimentaux. La première étape consiste ensuite à faire le bilan des forces qui s’appliquent sur le corps étudié (ici le « sous-marin »).
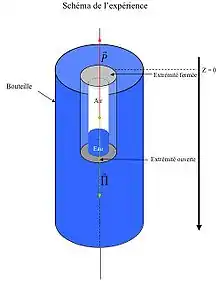
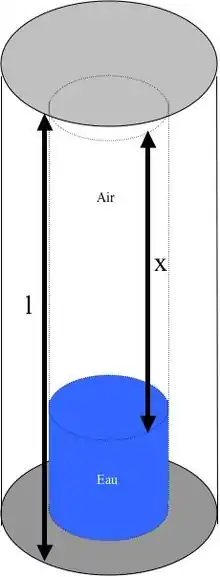
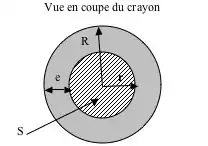
À l'extérieur du crayon
Bilan des forces qui s’appliquent sur le système crayon-trombone-air :
Il est soumis à deux forces :
- Son poids noté (dirigé vers le bas) : il a tendance à faire couler le système.
- Avec :
- et
- Notations :
- g = Accélération de la pesanteur
- = Masse volumique
- V = Volume
- m = Masse
- On obtient :
- La poussée d’Archimède notée (dirigée vers le haut) : elle a tendance à faire flotter le système.
- On obtient :
Remarque : on néglige la poussée d’Archimède sur le lest étant donné le faible volume occupé par celui-ci.
Pour commencer, on considère le système à l’équilibre et on applique la première loi de Newton. Les forces sont toutes parallèles à l'axe z donc :
On obtient
soit
- (1)
On pose
À présent, on se place dans le cas réel où le système ne se trouve pas forcément à l’équilibre. Ces forces se compensent alors plus ou moins. C’est ce qui provoque les mouvements du système dans la bouteille :
- le système monte lorsque : ;
- le système descend lorsque : ;
- le système est immobile lorsque : .
La constante représente donc la hauteur limite de la colonne d’air à l’intérieur du stylo en deçà de laquelle le système descend au fond de la bouteille. On peut donc prévoir, en observant le niveau d'eau dans le crayon et augmentant progressivement la pression de la main sur la bouteille, le moment où le « sous-marin va plonger ».
On sait donc maintenant que c’est le volume d’air à l’intérieur du stylo qui conditionne le mouvement du système. Car seule la poussée d’Archimède, qui dépend de ce volume, peut contrer les effets de l’attraction gravitationnelle. C’est bien le phénomène que l’on observe lors de l’expérience : lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du crayon et le système descend.
Il se pose alors une nouvelle question : pourquoi le fait d’appuyer fait-il varier le niveau d’eau dans le crayon ?
À l'intérieur du crayon
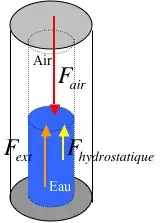
Pour répondre à la question précédente, nous allons maintenant nous intéresser aux forces qui s’exercent sur la surface d’eau en contact avec l’air à l’intérieur du crayon. Ces forces résultent de la pression de l’air et de l’eau à cet endroit.
Pour simplifier le problème, nous considérons l’air comme un gaz parfait. Nous pouvons donc déterminer la pression Pair à partir de la relation des gaz parfaits : PV = nRT où :
- P est la pression du gaz (Pa) ;
- V est le volume occupé par le gaz (m3) ;
- n est la quantité de gaz contenu dans ce volume (mole) ;
- R est la constante des gaz parfaits : R = 8,314 Pa⋅m3⋅mol-1⋅K-1 ;
- T est la température du gaz (K).
Au départ, avant de plonger le stylo dans l’eau, le crayon contient moles de gaz à la pression atmosphérique Patm , d’où
avec V : le volume intérieur (« vide ») du crayon
- .
Et lorsque l’on plonge le stylo dans l’eau, la même quantité d’air est contenue à l’intérieur de celui-ci. En revanche, on remarque qu’à présent il y a un peu d’eau dans le crayon. Toujours d’après la loi des gaz parfaits, étant donné que seul le volume occupé par l’air a diminué, c’est la pression qui a augmenté :
d’où
- .
Attention : cette relation est fausse, en effet on ne peut pas appliquer ainsi la loi des gaz parfaits. On peut considérer la conservation de la quantité d'air mais la transformation de l'air n'est pas isotherme, c'est-à-dire pas à température constante. Par contre, on peut considérer la transformation rapide et sans échange de chaleur, il vaut mieux modéliser la réaction de l'air par un adiabatique réversible et utiliser la loi :
- P⋅Va = constante
avec a le rapport des capacités calorifiques à pression et volume constant (on peut aussi considérer a constant dans cette étude).
Pour de plus amples détails et précision, référez-vous au programme de thermodynamique de première année de mathématiques supérieures.
Intéressons nous maintenant à la pression exercée par la surface d’eau sur la surface d’air. Celle-ci se décompose en deux parties : la pression hydrostatique (celle subit par les plongeurs) et la pression exercée par le manipulateur. Si on considère l’eau comme un fluide incompressible, alors la totalité de la force exercée sur les parois de la bouteille est transmise sur la surface air-eau.
- La pression hydrostatique est donnée par : .
- La pression exercée par le manipulateur sur le fluide est donnée par : .
D’où
- .
Prenons le système à l’équilibre : Fair = Feau. Ces deux forces s’exercent sur une même surface. On en déduit que : Pair = Peau, d’où
- .
On vient donc de relier la hauteur de la colonne d’air dans le stylo avec la pression exercée par le manipulateur sur la bouteille.
Conclusion
En combinant les équations (1) et (2), on peut alors définir la valeur minimum F0 de Fext nécessaire pour faire couler le stylo :
- .
Pour résumer :
- le système monte lorsque : F0 < Fext ;
- le système descend lorsque : F0 > Fext ;
- le système est immobile lorsque : F0 = Fext.
Notes et références
- Le coefficient de compressibilité de l'air à pression atmosphérique vaut environ 10−5 Pa-1, et celui de l'eau environ 5⋅10−10 Pa-1, l'eau est donc vingt mille fois moins compressible que l'air.
Voir aussi
Liens externes
- [vidéo] Une vidéo de l'expérience du ludion sur YouTube
























![{\displaystyle \textstyle \mathrm {F} _{0}=(\pi r^{2})[\rho _{\mathrm {eau} }gz+\mathrm {P_{atm}} (1-x_{0})]}](https://img.franco.wiki/i/d432172d21059922da9ea21fa772195cfa2ff7a5.svg)