Inégalité de Ptolémée

Figure de l'inégalité de Ptolémée.

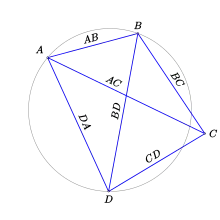
Théorème — Soient ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ et ${\displaystyle D}$ quatre points d'un espace affine euclidien. Alors,

${\displaystyle AC\cdot BD\leqslant AB\cdot CD+BC\cdot AD}$

avec égalité si et seulement si ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ et ${\displaystyle D}$ sont cocycliques ou alignés avec ${\displaystyle A}$, ${\displaystyle C}$ séparant ${\displaystyle B}$,${\displaystyle D}$.

Le cas d'égalité étant connu comme le théorème de Ptolémée.

L'inégalité de Ptolémée est la manifestation de l'inégalité triangulaire après l'application d'une inversion de centre l'un des points[1], ou, dans le cas plan, directement en utilisant les nombres complexes [2] - [1].

Soient ${\displaystyle a,b,c,d}$ les affixes respectives de ${\displaystyle A,B,C,D}$. En développant et refactorisant ${\displaystyle (b-a)(d-c)+(d-a)(c-b)}$, on obtient ${\displaystyle (c-a)(d-b)}$, donc d'après l'inégalité triangulaire, on a :

${\displaystyle AB\cdot CD+AD\cdot BC=|b-a||d-c|+|d-a||c-b|\geqslant |c-a||d-b|=AC\cdot BD}$, d'où l'inégalité voulue.

Si deux points sont confondus, les quatre points sont cocycliques ou alignés, sinon le cas d'égalité s'écrit :

${\displaystyle (b-a)(d-c)=\lambda (d-a)(c-b)}$ avec ${\displaystyle \lambda >0}$ , ce qui s'écrit aussi ${\displaystyle {\frac {b-a}{d-a}}=\lambda {\frac {c-b}{d-c}}}$, ou encore ${\displaystyle {\widehat {({\overrightarrow {AB}},{\overrightarrow {AD}})}}={\widehat {({\overrightarrow {BC}},{\overrightarrow {CD}})}}}$, d'où le résultat.

Soit ${\displaystyle A'}$, ${\displaystyle B'}$ et ${\displaystyle C'}$ les images respectives de ${\displaystyle A}$, ${\displaystyle B}$ et ${\displaystyle C}$ par l'inversion de centre ${\displaystyle D}$ et de rapport ${\displaystyle 1}$.

Nous avons les relations entre longueurs :

${\displaystyle A'B'={\frac {AB}{DA\times DB}}}$

${\displaystyle B'C'={\frac {BC}{DC\times DB}}}$

${\displaystyle A'C'={\frac {AC}{DA\times DC}}}$

Ainsi l'inégalité triangulaire ${\displaystyle A'C'\leqslant A'B'+B'C'}$ nous donne

${\displaystyle {\frac {AC}{DA\times DC}}\leqslant {\frac {AB}{DA\times DB}}+{\frac {BC}{DC\times DB}}}$

qui après multiplication par ${\displaystyle DA\times DB\times DC}$ devient

${\displaystyle AC\times BD\leqslant AB\times CD+BC\times AD}$

Il y a égalité si et seulement si ${\displaystyle A'}$, ${\displaystyle B'}$ et ${\displaystyle C'}$ sont alignés dans cet ordre, ce qui est équivalent à : ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ et ${\displaystyle D}$ sont cocycliques ou alignés, avec ${\displaystyle A,C}$ séparant ${\displaystyle B,D}$.