Inégalité de Jordan

En mathématiques, l'inégalité de Jordan, du nom du mathématicien Camille Jordan, est la suivante [1]

{\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ pour }}x\in \left[0,{\frac {\pi }{2}}\right].

{\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ pour }}x\in \left[0,{\frac {\pi }{2}}\right]

Le cercle unité au centre, et un cercle de rayon

|EG|=\sin(x)

centré sur E.

{\begin{aligned}&|DE|\leq |{\widehat {DC}}|\leq |{\widehat {DG}}|\\\Leftrightarrow &\sin(x)\leq x\leq {\tfrac {\pi }{2}}\sin(x)\\\Rightarrow &{\tfrac {2}{\pi }}x\leq \sin(x)\leq x\end{aligned}}

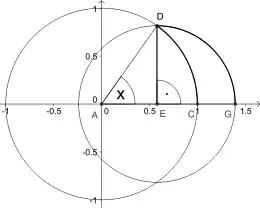
Cela peut être prouvé géométriquement comme ci-dessous[2].

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jordan's inequality » (voir la liste des auteurs).
1. (en) Eric W. Weisstein, « {{{titre}}} », sur MathWorld
2. Nach Feng Yuefeng, La preuve sans mots: l'inégalité de Jordan, Mathematics Magazine, volume 69, no. 2, 1996, p. 126

Serge Colombo: Fonctions holomorphes d'une variable . Taylor & Francis 1983, (ISBN 0677059507) , p. 167-168 ( copie en ligne )
Da-Wei Niu, Jian Cao, Feng Qi: Généralisations de l'inégalité de la Jordanie et des relations concernées UPB Sci. Bull., Série A, Volume 72, Numéro 3, 2010, (ISSN 1223-7027)
Feng Qi: l'inégalité de la Jordanie: raffinements, généralisations, applications et problèmes connexes RGMIA Res Rep Coll (2006), Volume 9, Numéro: 3, Pages: 243–259
Meng-Kuang Kuo: Raffinements de l'inégalité de la Jordanie Journal des inégalités et des applications 2011, 2011: 130, doi: 10.1186 / 1029-242X-2011-130

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.