Formule de Kelly

Pour les paris simples avec uniquement deux résultats, l'un impliquant de perdre le montant de sa mise, et l'autre impliquant de gagner le montant de la mise multiplié par la cote des gains, le pari Kelly est le suivant :

${\displaystyle f^{*}={\frac {bp-q}{b}}=p-q/b}$,

où :

• f * est la fraction du budget courant à parier ;
• b est la cote nette reçue sur le pari (c'est-à-dire le rapport généralement exprimé comme « b contre 1 ») ;
• p est la probabilité de gain ;
• q est la probabilité de perdre, égale à (1 - p).

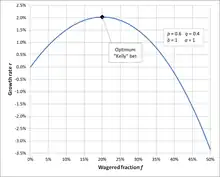
À titre d'exemple, si un pari offre 60 % de chance de gagner la mise (p = 0,60, q = 0,40, b = 1), alors le joueur doit miser 20 % de son budget à chaque opportunité (f * = 0,20), afin de maximiser les taux à long terme de croissance de son capital.

Si le joueur n'a aucun avantage (son gain statistique moyen égale sa perte statistique moyenne), c'est-à-dire si b = q / p, alors la règle est de ne rien parier.

Si le joueur a un désavantage (son gain statistique moyen est inférieur à sa perte statistique moyenne) (b < q / p) la formule donne un résultat négatif, indiquant que le joueur devrait prendre l'autre côté du pari (à la roulette, cela signifie que le joueur devrait se mettre à la place de la banque).

Par exemple, dans la roulette standard, le parieur double son gain (b = 1) sur le rouge. Or il y a 18 numéros rouges et 19 numéros non rouge sur la roue (p = 18/37), donc le joueur a moins d'une chance sur deux de gagner. Le pari Kelly est −1/37, autrement dit le joueur doit miser un trente-septième de son capital contre (et non sur) le rouge. Malheureusement, le casino ne permet pas de parier contre le rouge, donc la formule de Kelly recommande alors de ne pas jouer (la mise négative étant impossible).

Pour ces paris 1 contre 1 (c'est-à-dire quand b = 1), la formule peut être simplifiée en :

${\displaystyle f^{*}=p-q}$.

Comme q = 1-p, ceci se simplifie en :

${\displaystyle f^{*}=2p-1}$.

Pour les paris avec uniquement deux résultats, l'un impliquant de perdre une partie c de sa mise (c<1), et l'autre impliquant de gagner le montant de la mise multiplié par la cote des gains b, le pari Kelly devient :

${\displaystyle f^{*}={p/c-q/b}}$,

à condition que l'espérance du pari pb - qc soit positive.

Dans ce cas, il est justifiable d'emprunter une partie de la mise (levier), mais jamais plus que la partie (1-c) qui n'est pas en risque. Le montant optimal à emprunter dépend bien sûr du taux d'intérêt.

Exemple : pari mutuel sur les courses de chevaux. Chaque cheval i a une probabilité ${\displaystyle p_{i}}$ de gagner, mais une cote ${\displaystyle b_{i}}$ en cas de gain.

Il n'y a pas de formule simple. On doit calculer les mises optimales en appliquant le critère de Kelly. Elles auront pour propriété que :

${\displaystyle f_{i}^{*}=p_{i}-R/b_{i}}$ si c'est positif,

${\displaystyle f_{i}^{*}=0}$ sinon,

où ${\displaystyle R=1-\sum f_{i}^{*}={\frac {1-\sum _{f_{i}^{*}>0}p_{i}}{1-\sum _{f_{i}^{*}>0}b_{i}}}}$ est le budget non investi.

Une méthode itérative consiste à commencer par sélectionner le « cheval » pour lequel ${\displaystyle p_{i}-1/b_{i}}$ est le plus élevé et y allouer (provisoirement) cette part du budget. On calcule R, on cherche le deuxième « cheval » le plus intéressant et on recalcule les parts de budget à allouer aux deux chevaux. En recommençant cheval après cheval, on arrête lorsqu'il n'y a plus de cheval intéressant. La répartition atteinte à ce moment est celle de Kelly.

Le critère permet aussi de décider quelle part du budget allouer à chaque pari/investissement.

Il faut considérer toutes les combinaisons de résultats et appliquer la règle ci-dessus. Le résultat ne se prête pas à une formulation simple.

En général, le critère recommande de diversifier (réduire le risque).