Fonction de hachage parfait
En informatique, une fonction de hachage parfait h pour un ensemble S est une fonction de hachage qui associe des éléments distincts de S à un ensemble de m entiers, sans collisions. En termes mathématiques, c'est une fonction injective.
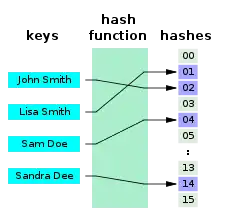
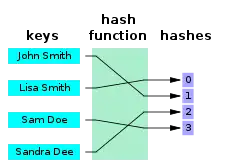
Des fonctions de hachage parfait peuvent être utilisées pour implémenter une table de correspondance avec un temps d'accès constant dans le pire des cas. Une fonction de hachage parfait peut, comme toute fonction de hachage, être utilisée pour implémenter des tables de hachage, avec l'avantage qu'aucun mécanisme de résolution de collisions ne doit être implémenté. De plus, si les clés ne sont pas des données utiles et si l'on sait que les clés interrogées seront valides, les clés n'ont pas besoin d'être stockées dans la table de correspondance, ce qui permet d'économiser de l'espace mémoire.
Un inconvénient des fonctions de hachage parfait est que S doit être connu pour la construction de la fonction de hachage parfait. Les fonctions de hachage parfait non dynamiques doivent être reconstruites si S change. Pour changer fréquemment S, des fonctions de hachage parfait dynamiques peuvent être utilisées au prix d'un espace supplémentaire. L'espace requis pour stocker la fonction de hachage parfait est en O(n).
Les paramètres de performance importants pour les fonctions de hachage parfait sont le temps d'évaluation, qui doit être constant, le temps de construction et la taille mémoire de la représentation.
Applications
Une fonction de hachage parfait avec des valeurs dans une plage limitée peut être utilisée pour des opérations de recherche efficaces, en plaçant les clés de S (ou d'autres valeurs associées) dans une table de correspondance indexée par les valeurs de sortie de la fonction. On peut alors tester si une clé est présente dans S, ou rechercher une valeur associée à cette clé, en la recherchant dans sa cellule du tableau. Chacune de ces recherches prend un temps constant dans le pire des cas. Avec un hachage parfait, les données associées peuvent être lues ou écrites avec un seul accès à la table.
Performance des fonctions de hachage parfait
Les paramètres importants de performance pour un hachage parfait sont la taille de représentation, le temps d'évaluation, le temps de construction et, en outre, le ratio où m est le nombre de cellules, et n le nombre d'éléments dans la structure de données. Le temps d'évaluation peut être aussi rapide que O(1), ce qui est optimal[1]. Le temps de construction est d'au moins O(n), car chaque élément de S doit être pris en compte et S contient n éléments. Cette borne inférieure peut être atteinte en pratique[1].
La borne inférieure de la taille mémoire de représentation de la fonction de hachage dépend de m et n. Soit m = (1+ε) n et h une fonction de hachage parfait. Une bonne approximation de la borne inférieure est bits par élément. Pour un hachage parfait minimal, i.e. pour ε = 0, la borne inférieure est bits par élément.
Construction
Une fonction de hachage parfait pour un ensemble spécifique S qui peut être évalué en temps constant, et avec des valeurs dans une petite plage, peut être trouvée par un algorithme probabiliste dans un nombre d'opérations qui est proportionnel à la taille de S. La construction originale de Fredman, Komlós & Szemerédi (1984) utilisent un schéma à deux niveaux pour envoyer un ensemble S de n éléments sur une plage de O(n) indices, puis envoyer chaque indice sur une plage de valeurs de hachage. Le premier niveau de leur construction choisit un grand nombre premier p (plus grand que la taille de l'univers à partir duquel S est tiré), et un paramètre k, et fait correspondre chaque élément x de S à l'indice
Si k est choisi au hasard, cette étape est susceptible d'avoir des collisions, mais le nombre d'éléments ni qui sont simultanément envoyés au même indice i a de grandes chances d'être petit. Le deuxième niveau de leur construction attribue des plages disjointes d'entiers de taille O(ni2) à chaque indice i. Il utilise un deuxième ensemble de fonctions modulaires linéaires, une pour chaque index i, pour mapper chaque membre x de S dans la plage associée à g(x).
Comme le montrent Fredman, Komlós & Szemerédi (1984)[2], il existe un choix du paramètre k tel que la somme des longueurs des plages pour les n valeurs différentes de g(x) soit en O(n). De plus, pour chaque valeur de g(x), il existe une fonction modulaire linéaire qui envoie le sous-ensemble correspondant de S dans la plage associée à cette valeur.La valeur de k et les fonctions de second niveau pour chaque valeur de g(x), peuvent être trouvées en temps polynomial en choisissant des valeurs au hasard jusqu'à en trouver une qui fonctionne.
La fonction de hachage elle-même nécessite un espace de stockage O(n) pour stocker k, p et toutes les fonctions modulaires linéaires de second niveau. Le calcul de la valeur de hachage d'une clé donnée x peut être effectué en temps constant en calculant g(x), en recherchant la fonction de second niveau associée à g(x) et en appliquant cette fonction à x. Une version modifiée de ce schéma à deux niveaux avec un plus grand nombre de valeurs au niveau supérieur peut être utilisée pour construire une fonction de hachage parfait qui envoie S dans une plage plus petite de longueur n + o(n).
Une méthode plus récente pour construire une fonction de hachage parfait est décrite par Belazzougui, Botelho & Dietzfelbinger (2009)[1] comme "hacher, déplacer et compresser". Ici, une fonction de hachage de premier niveau g est également utilisée pour envoyer des éléments sur une plage de r entiers. Un élément x ∈ S est stocké dans le Bucket Bg(x).
Ensuite, par ordre décroissant de taille, les éléments de chaque bucket sont hachés par une fonction de hachage d'une séquence de fonctions de hachage entièrement aléatoires indépendantes (Φ1, Φ2, Φ3, ...), en commençant par Φ1. Si la fonction de hachage ne produit aucune collision pour le bucket et que les valeurs résultantes ne sont pas encore occupées par d'autres éléments d'autres buckets, la fonction est choisie pour ce bucket. Si ce n'est pas le cas, la fonction de hachage suivante de la séquence est testée.
Pour évaluer la fonction de hachage parfait h(x), il suffit de sauvegarder le l'image σ de l'indice de compartiment g(x) sur la fonction de hachage correcte dans la séquence, ce qui donne h(x) = Φσ(g(x)).
Enfin, pour réduire la taille de la représentation, les ( σ(i))0 ≤ i < r sont compressés sous une forme qui permet toujours l'évaluation en O(1).
Cette approche nécessite un temps linéaire en n pour la construction, et permet un temps d'évaluation constant. La taille de la représentation est en O(n), et dépend de la plage atteinte. Par exemple, avec m = 1.23n Belazzougui, Botelho & Dietzfelbinger (2009) ont atteint une taille de représentation comprise entre 3,03 bits/clé et 1,40 bits/clé pour leur exemple donné de 10 millions d'entrées, les valeurs inférieures nécessitant un temps de calcul plus élevé. La limite inférieure de l'espace dans ce scénario est de 0,88 bit/clé.
Pseudocode
l'algorithme de hachage, de déplacement et de compression est (1) Diviser S en paquets Bi := g−1({i})∩S,0 ≤ i < r (2) Trier les paquets Bi par ordre décroissant selon la taille |Bi| (3) Initialiser le tableau T[0...m-1] avec des 0 (4) pour tout i ∈[r], dans l'ordre de (2), faire (5) pour l ← 1,2, ... (6) répéter la construction de Ki ← Φl(x)|x ∈ Bi} (6) tant que |Ki|≠|Bi| ou Ki∩{j|T[j]=1}≠ ∅ (7) soit σ(i):= le l réussi (8) pour tout j ∈ Ki laisse T[j]:= 1 (9) Transformer (σi)0≤i<r sous forme compressée, en conservant l'accès O(1).
Limites inférieures en espace
Le stockage de la fonction de Fredman, Komlós & Szemerédi (1984)[2] en O(n) est quasi optimal : toute fonction de hachage parfait calculable en temps constant nécessite au moins un nombre de bits proportionnel à la taille de S.
Pour les fonctions de hachage parfait minimal, la borne inférieure théorique de l'espace de stockage est
bits par clé.
Pour les fonctions de hachage parfait, on définit ε tel que la taille de la plage de h est m = (1+ε) n. Avec la formule donnée par Belazzougui, Botelho & Dietzfelbinger (2009)[1] et pour un univers dont la taille |U| = u tend vers l'infini, le minorant de l'espace est
bits par clé, moins log(n) bits au total.
Extensions
Identité de l'adresse mémoire
Un exemple trivial mais omniprésent de hachage parfait est implicite dans l'adresse mémoire (virtuelle) d'un ordinateur. Étant donné que chaque octet de mémoire virtuelle est un emplacement de stockage distinct, unique et directement adressable, la valeur de l'adresse de départ de tout objet stocké en mémoire peut être considérée comme un hachage parfait de facto de cet objet dans toute la plage d'adresses mémoire[3].
Hachage parfait dynamique
L'utilisation d'une fonction de hachage parfait est préférable dans les situations où il existe un grand ensemble fréquemment interrogé, S, qui est rarement mis à jour. En effet, toute modification de l'ensemble S peut rendre le hachage non parfait pour l'ensemble modifié. Les solutions qui mettent à jour la fonction de hachage chaque fois que l'ensemble est modifié sont connues sous le nom de hachage parfait dynamique, mais ces méthodes sont relativement compliquées à mettre en œuvre.
Fonction de hachage parfait minimale
Une fonction de hachage parfait minimal est une fonction de hachage parfait qui envoie n clés sur n entiers consécutifs - généralement les nombres de 0 à n − 1 ou de 1 à n. Une manière plus formelle d'exprimer cela est la suivante : Soient j et k des éléments d'un ensemble fini S. Alors h est une fonction de hachage parfait minimale si et seulement si h(j) = h(k) implique j = k ( injectivité ) et il existe un entier a tel que la plage de h soit a..a + |S| − 1. Il a été prouvé qu'un schéma de hachage parfait minimal à usage général nécessite au moins lg e ≈ 1.44 bits/clé. Bien que cette limite d'espace ait été atteinte par des travaux théoriques, en pratique, les schémas de hachage parfait minimal les plus connus nécessitent environ 1,56 bits/clé si on leur donne suffisamment de temps.
hachage k-parfait
Une fonction de hachage est k -parfait si au plus k éléments de S sont envoyés sur la même valeur dans la plage. L'algorithme "hacher, déplacer et compresser" peut être utilisé pour construire des fonctions de hachage k -parfait en autorisant jusqu'à k collisions. Les modifications nécessaires pour y parvenir sont minimes et sont soulignées dans le pseudocode adapté ci-dessous :
(4) pour tout i ∈[r], dans l'ordre de (2), faire
(5) pour l ← 1,2, ...
(6) répéter la formation de Ki ← Φl(x)|x ∈ B je }
(6) jusqu'à |K i |=|B i | et Ki∩{j| T[j]=k }= ∅
(7) soit σ(i):= le l réussi
(8) pour tout j ∈ Ki fixer T[j] ← T[j]+1
Préservation de la commande
Une fonction de hachage parfait minimal F préserve l'ordre si les clés sont données dans un certain ordre a1, a2, ..., an et pour toutes les clés aj et ak, j < k implique F(aj) < F(ak). Dans ce cas, la valeur de la fonction est simplement la position de chaque clé dans l'ordre trié de toutes les clés. Une implémentation simple des fonctions de hachage parfait minimal préservant l'ordre avec un temps d'accès constant consiste à utiliser une fonction de hachage parfait (ordinaire) ou un hachage coucou pour stocker une table de recherche des positions de chaque clé. Si les clés à hacher sont elles-mêmes stockées dans un tableau trié, il est possible de stocker un petit nombre de bits supplémentaires par clé dans une structure de données qui peut être utilisée pour calculer rapidement des valeurs de hachage. Les fonctions de hachage parfait minimal préservant l'ordre nécessitent nécessairement Ω(n log n) bits pour être représentées.
Constructions connexes
Une alternative simple au hachage parfait, qui permet également des mises à jour dynamiques, est le hachage cuckoo. Ce schéma envoie les clés à deux emplacements ou plus dans une plage (contrairement au hachage parfait qui envoie chaque clé à un seul emplacement) mais le fait de telle manière que les clés peuvent être attribuées une à une aux emplacements auxquels elles ont été envoyées. Les recherches avec ce schéma sont plus lentes, car plusieurs emplacements doivent être vérifiés, mais prennent néanmoins un temps constant dans le pire des cas.
Notes et références
- (en) Djamal Belazzougui, Fabiano C. Botelho et Martin Dietzfelbinger, « Algorithms—ESA 2009: 17th Annual European Symposium, Copenhagen, Denmark, September 7-9, 2009, Proceedings », Lecture Notes in Computer Science, (DOI 10.1007/978-3-642-04128-0_61, lire en ligne)
- (en) Michael L. Fredman, János Komlós et Endre Szemerédi, « Storing a Sparse Table with 0 (1) Worst Case Access Time », Journal of the ACM, vol. 31, no 3, , p. 538–544 (ISSN 0004-5411 et 1557-735X, DOI 10.1145/828.1884, lire en ligne, consulté le )
- Witold Litwin, Tadeusz Morzy et Gottfried Vossen, Advances in Databases and Information Systems, Springer Science+Business Media, (ISBN 9783540649243, lire en ligne), p. 254
Lectures complémentaires
- Richard J. Cichelli. Fonctions de hachage parfaites minimales simplifiées, Communications de l'ACM, Vol. 23, numéro 1, janvier 1980.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein. Introduction aux algorithmes, troisième édition. Presse du MIT, 2009. (ISBN 978-0262033848). Section 11.5 : Hachage parfait, p. 267, –.
- Fabiano C. Botelho, Rasmus Pagh et Nivio Ziviani. " Hachage parfait pour les applications de gestion de données ".
- Fabiano C. Botelho et Nivio Ziviani. "Hachage externe parfait pour les très grands ensembles de clés". 16th ACM Conference on Information and Knowledge Management (CIKM07), Lisbonne, Portugal, novembre 2007.
- Djamal Belazzougui, Paolo Boldi, Rasmus Pagh et Sebastiano Vigna. "Hachage parfait minimal monotone: recherche d'une table triée avec des accès O (1)". Dans Actes du 20e symposium annuel ACM-SIAM sur les mathématiques discrètes (SODA), New York, 2009. Presse ACM.
- Marshall D. Brain et Alan L. Tharp. "Hachage presque parfait de grands ensembles de mots". Logiciel—Pratique et expérience, vol. 19(10), 967-078, octobre 1989. John Wiley et fils.
- Douglas C. Schmidt, GPERF : un générateur de fonction de hachage parfait, rapport C++, SIGS, vol. 10, no 10, novembre/décembre 1998.
Liens externes
- gperf est un générateur de hachage parfait Open Source C et C ++ (très rapide, mais ne fonctionne que pour de petits ensembles)
- Hachage parfait minimal (algorithme bob) par Bob Jenkins
- cmph : C Minimal Perfect Hashing Library, implémentations open source pour de nombreux hachages parfaits (minimaux) (fonctionne pour les grands ensembles)
- Sux4J : hachage parfait minimal monotone open source en Java
- MPHSharp : méthodes de hachage parfaites en C#
- BBHash : fonction de hachage parfaite minimale en C++ avec en-tête uniquement
- Perfect::Hash, générateur de hachage parfait en Perl qui crée du code C. A une section "art antérieur" qui vaut la peine d'être consultée.






