Ellipsoïde de Fresnel
L’ellipsoïde de Fresnel est un volume dans l'espace permettant d'évaluer l'atténuation apportée par un obstacle (immeuble, colline...) à la propagation d'une onde mécanique ou électromagnétique. Il est généralement utilisé dans le cas de liaisons VHF, UHF ou hyperfréquences, qui seraient en espace libre sans la présence du ou des obstacles. La méthode de l'ellipsoïde de Fresnel permet alors d'évaluer l'atténuation supplémentaire apportée par l'obstacle.
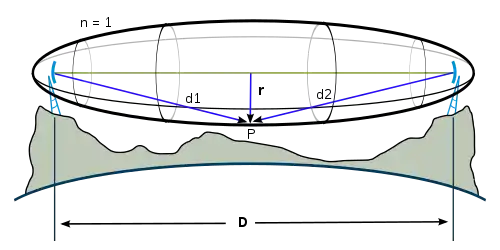
Définition
Soient A l'antenne d'émission et B l'antenne de réception, pour une émission radio de longueur d'onde .
On considère les points M de l'espace tels que . Avec comme l'image ci-contre, il s'agit de ce qu'on appelle le premier ellipsoïde de Fresnel. Le lieu de ces points est un ellipsoïde de foyers A et B.
Si est la distance AB entre les antennes, au centre de la liaison (c'est-à-dire autour du milieu de AB), le rayon de cet ellipsoïde est égal à :
Physiquement, on peut dire que si les obstacles se trouvent tous à l'extérieur de cet ellipsoïde, ils n'auront pratiquement aucune influence sur l'onde directe reçue par l'antenne de réception. Autrement dit, l'ellipsoïde représente la partie de l'espace suffisante à la propagation en espace libre entre les deux antennes.
A contrario, si des obstacles sont présents à l'intérieur de cet espace, il faudra s'attendre à une atténuation supplémentaire par rapport à la propagation en espace libre.
Lorsque l'obstacle se trouve nettement plus près de l'une des antennes, on peut approcher l'ellipsoïde par un paraboloïde dont le foyer est l'antenne concernée. Il est alors commode de calculer le rayon de l'ellipsoïde à une distance de l'antenne ( petit devant ) :
la deuxième approximation suppose que est petit devant .
Propriétés
Il est possible d'évaluer l'atténuation supplémentaire apportée par l'obstacle, notamment si celui-ci est étroit.
Appelons la distance entre le sommet de l'obstacle et la droite de liaison AB.
Ainsi, si un obstacle est juste tangent à la ligne de liaison AB (), il obstrue le demi-cercle inférieur. L'atténuation est alors de 6 dB.
Si l'obstacle a une hauteur telle qu'il obstrue juste la totalité du cercle (), l'atténuation sera de 14 dB environ.
Si l'obstacle effleure juste l'ellipsoïde (), on observe un gain de l'ordre de 1 dB par rapport à la propagation en espace libre...
Atténuation en fonction de :
- si alors At = 6 dB
- si alors At = 14 dB
- si alors At = 20 dB
Si l'obstacle est épais, il faudra compter sur une atténuation supplémentaire.
Exemple
Soit une antenne de faisceau hertzien émettant sur 4 cm (7,5 GHz) de longueur d'onde. À 100 mètres de l'antenne, se trouve un immeuble empêchant la visibilité optique. Si on trace une droite entre les antennes, on constate que l'immeuble dépasse de 2 mètres au-delà de cette ligne.
On calcule le rayon de l’ellipsoïde à cet endroit, avec et :
Donc et l'atténuation apportée par l’immeuble est de 14 dB.
Cette atténuation est à ajouter à celle calculée « en espace libre » : voir Propagation des ondes radio dans l'espace
Conditions d'utilisation
Si l'obstacle est étroit et s’il est unique, la méthode de l'ellipsoïde permet d'évaluer les pertes apportées par l'obstacle. En plus du relief, il faudra bien sûr tenir compte de la courbure de la Terre si la liaison dépasse quelques kilomètres.
Bien sûr, l'obstacle devra être suffisamment éloigné de l'antenne pour considérer que l'on est en onde plane.
Si l'obstacle (en général le relief) empiète l'ellipsoïde en plusieurs endroits, ou sur une distance importante, seul un logiciel de simulation de bilan de liaison permettra de calculer l'atténuation avec précision.

















