Duolet

Dans le solfège, le duolet est une division exceptionnelle du temps formée d'un groupe de deux figures égales dont la somme équivaut à trois figures identiques dans un temps normalement ternaire.

Le duolet est signalé par le chiffre « 2 » placé au-dessus ou au-dessous du groupe concerné.

On trouve donc le duolet à la place d'un temps ternaire.

On peut également trouver le duolet sur un groupe de trois temps consécutifs (rarement davantage). Si par exemple la noire est l'unité de temps, il est possible, de remplacer trois noires ordinaires par deux noires en duolet, dont la somme équivaut à trois temps, soit, la valeur d'une blanche pointée.

Contrairement à ce qui se passe pour le triolet, on ne trouve jamais de duolet sur une partie de temps, puisqu'une partie de temps est toujours représentée par une valeur simple, donc, binaire, c'est-à-dire, naturellement divisible par deux.

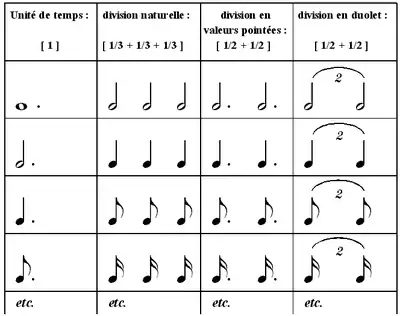
Si l'on se réfère aux tableaux des valeurs relatives des figures pointées, le duolet peut être remplacé par deux valeurs pointées correspondantes.

Au sein d'un duolet, la blanche vaut la moitié d'une ronde pointée, la noire vaut la moitié d'une blanche pointée, la croche vaut la moitié d'une noire pointée, etc.

Un duolet peut ne pas former un groupe de deux notes égales, il suffit que la somme de ses durées soit équivalente à celle des deux notes égales. Par ailleurs, un duolet peut contenir des silences : la valeur du silence est alors égale à celle de la note qu'il remplace. Ainsi, chaque duolet de l'exemple ci-dessous équivaut à une noire pointée, soit à un duolet de croches :

Duolet signifie ainsi deux au lieu de trois, ou encore, deux en l'espace de trois.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.