Dîner des philosophes
Le problème du « dîner des philosophes » est un cas d'école classique sur le partage de ressources en informatique système. Il concerne l'ordonnancement des processus et l'allocation des ressources à ces derniers et a été énoncé par Edsger Dijkstra[1].
Le problème

La situation est la suivante :
- Cinq philosophes (initialement, mais il peut y en avoir beaucoup plus) se trouvent autour d'une table ;
- Chacun des philosophes a devant lui un plat de spaghettis ;
- À gauche de chaque plat de spaghettis se trouve une fourchette.
Un philosophe n'a que trois états possibles :
- Penser pendant un temps indéterminé ;
- Être affamé pendant un temps déterminé et fini (sinon il y a famine) ;
- Manger pendant un temps déterminé et fini.
Des contraintes extérieures s'imposent à cette situation :
- Pour manger, un philosophe a besoin de deux fourchettes : celle qui se trouve à gauche de sa propre assiette, et celle qui se trouve à droite (c'est-à-dire les deux fourchettes qui entourent sa propre assiette) ;
- Quand un philosophe a faim, il va se mettre dans l'état « affamé » et attendre que les fourchettes soient libres ;
- Si un philosophe n'arrive pas à s'emparer d'une fourchette, il reste affamé pendant un temps déterminé, en attendant de renouveler sa tentative.
Le problème consiste à trouver un ordonnancement des philosophes tel qu'ils puissent tous manger, chacun à leur tour. Cet ordre est imposé par la solution que l'on considère comme celle de Dijkstra avec sémaphores ou Courtois avec des compteurs.
Remarques
- Les philosophes, s'ils agissent tous de façon naïve et identique, risquent fort de se retrouver en situation d'interblocage. En effet, il suffit que chacun saisisse sa fourchette de gauche et, qu'ensuite, chacun attende que sa fourchette de droite se libère pour qu'aucun d'entre eux ne puisse manger, et ce pour l'éternité.
- On considère qu'un philosophe qui meurt (crash du processus) reste dans une phase « penser » infiniment. Il en résulte donc un problème : que dire d'un philosophe qui meurt avec ses fourchettes en main ?
- Pour plus de compréhension ce problème est aussi connu sous le nom de "problème des baguettes chinoises", où le philosophe a besoin de deux baguettes pour pouvoir manger.
Solutions
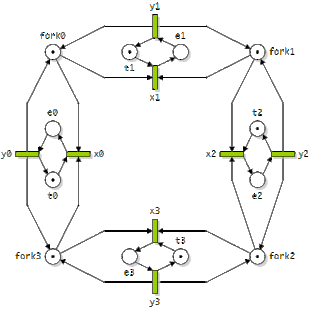
- L'une des principales solutions à ce problème est celle du sémaphore, proposée également par Dijkstra.
- Une autre solution consiste à attribuer à chaque philosophe un temps de réflexion aléatoire en cas d'échec (cette solution est en réalité incorrecte).
- Il existe des compromis qui permettent de limiter le nombre de philosophes gênés par une telle situation, notamment une toute simple se basant sur la technique hiérarchique de Havender qui limite le nombre de philosophes touchés à un d'un côté et deux de l'autre.
La solution de Chandy/Misra
En 1984, K. M. Chandy et J. Misra proposèrent une nouvelle solution permettant à un nombre arbitraire n d'agents identifiés par un nom quelconque d'utiliser un nombre m de ressources. Le protocole élégant et générique est le suivant :
- Pour chaque paire de philosophes pouvant accéder à la même fourchette, on commence par la donner à celui des deux qui a le plus petit nom (selon une certaine relation d'ordre). Toute fourchette est soit propre soit sale. Au début, toutes les fourchettes sont sales.
- Lorsqu'un philosophe veut manger, il doit obtenir les fourchettes de ses deux voisins. Pour chaque fourchette qui lui manque, il émet poliment une requête.
- Lorsqu'un philosophe qui a une fourchette en main entend une requête pour celle-ci,
- soit la fourchette est propre et il la garde.
- soit la fourchette est sale, alors il la nettoie et il la donne.
- Après qu'un philosophe a fini de manger, ses deux fourchettes sont devenues sales. Si un autre philosophe avait émis une requête pour obtenir une de ses fourchettes, il la nettoie et la donne.
Solution dans le cas pair
Dans le cas pair une solution simple existe. On numérote les philosophes selon leur place à la table. Et l'on décide que les philosophes ayant un nombre pair prennent d'abord leur fourchette gauche, puis leur droite et l'inverse avec les philosophes ayant un nombre impair.
Preuve de l'exactitude de cette solution
Étudions le cas d'un philosophe qui prend d'abord sa fourchette gauche. S'il y arrive, il ne lui reste plus qu'à prendre sa fourchette droite. Celle-ci ne peut être définitivement bloquée : si le philosophe de droite la tient, c'est qu'il est en train de manger (il tient dans ce cas ses deux fourchettes). Ainsi nos philosophes ne se bloqueront jamais.
La compréhension de cette solution est plus aisée en prenant pour exemple la présence de deux philosophes.
Notes et références
- (en) Edsger W. Dijkstra, « Hierarchical ordering of sequential processes », Acta Informatica, vol. 1, , p. 115-138 (lire en ligne, consulté le )
Voir aussi
Articles connexes
Lien externe
- « Illustration du problème des philosophes »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ) (applet Java)
