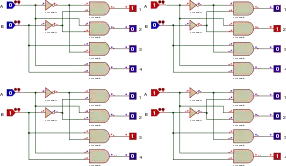
Démultiplexeur
Un démultiplexeur est un circuit combinatoire à N+1 entrées et 2N sorties. Les N entrées, appelées entrées d'adressage, permettent d'envoyer sur l'une des sorties la dernière entrée, appelée entrée de donnée.
Un décodeur est un cas particulier dans lequel on relie l'entrée donnée du démultiplexeur à 1. Le décodeur est donc un circuit combinatoire à N entrées et 2N sorties. Sélectionner une sortie grâce aux entrées d'adressage la fera passer de l'état 0 à l'état 1.
Cas du démultiplexeur
Table de vérité
Table de vérité d'un démultiplexeur 2+1 vers 4. Les entrées sont C1, C0 et D0, les sorties S0, S1, S2, S3.
| C1 | C0 | D0 | S0 | S1 | S2 | S3 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Schéma logique
Section vide
Cas du décodeur
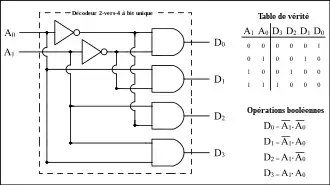
Table de vérité
Table de vérité d'un décodeur 2 vers 4, les entrées sont C1C0 et les sorties S0, S1, S2, S3. Le principe est d'activer ou désactiver une seule sortie par combinaison d'entrée.
| C1 | C0 | S0 | S1 | S2 | S3 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Schéma logique
Ci-dessous, un décodeur à 2 entrées et 4 sorties. La construction (voir les entrées des portes ET) suit la progression binaire : 00, 01, 10, 11.