Courbe de Lévy
En mathématiques, la courbe de Lévy ou courbe en C est une courbe fractale.
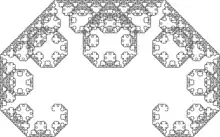
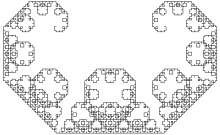
Décrite pour la première fois par Ernesto Cesàro en 1906[1] et Georg Faber en 1910[2], elle porte maintenant le nom du mathématicien français Paul Lévy qui, en 1938, a été le premier à décrire ses propriétés d'auto-similarité, et à en apporter une construction géométrique[3].
Propriétés
- La dimension de Hausdorff de la courbe de Lévy égale 2 (elle contient des ensembles ouverts). Résultat déduit directement de sa construction par deux homothéties de rapport 1/√2.
- Sa frontière a une dimension estimée à environ 1,9340[4].
- La courbe de Lévy pave le plan[5].
- Si le segment d'origine a pour longueur 1, l'aire recouverte par la courbe de Lévy vaut 1/4[5].
- La courbe de Lévy est un des six 2-autopavés réguliers (peut être pavée par deux copies d'elle-même, de même taille)[6].
- Elle est un cas particulier de la courbe de De Rham (en).
Construction par un système de Lindenmayer (L-système)
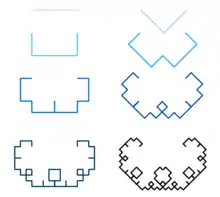
La construction de la courbe de Lévy part d'un segment de droite. Ce segment est remplacé par les deux côtés du triangle rectangle isocèle ayant le segment d'origine pour hypoténuse. A l'étape 2, la courbe est donc représentée par deux segments à angle droit. Par rapport au segment original ces deux segments sont réduits d'un facteur 1/√2.
On applique cette règle itérativement pour chaque nouveau segment créé.
Après n étapes, la courbe consiste en segments de longueur réduits d'un facteur par rapport au segment d'origine.
Le système de Lindenmayer associé peut ainsi être décrit comme suit :
Variables: F Constantes: + − Axiome: F Règles: F → +F−−F+
Où "F" signifie "avance tout droit", "+" signifie "tourne à droite à 45°", et "−" signifie "tourne à gauche à 45°".
L'ensemble limite de ce L-système est la courbe de Lévy.
Variantes
La courbe standard est construite en utilisant des angles de 45 degrés. On peut élaborer des variantes de cette courbe en utilisant des angles différents. Tant que l'angle reste inférieur à 60 degrés, les nouveaux segments créés à chaque étape restent inférieurs au segment d'origine et l'ensemble converge vers une courbe limite.
Construction par un système de fonctions itérées

La construction d'une courbe de Lévy par un système de fonctions itérées s'appuie sur un ensemble de deux fonctions linéaires contractantes de rapport 1/√2[7]. La première introduit une rotation de 45°, la deuxième une rotation de -45°.
La courbe de Lévy C dans le plan complexe peut donc être définie comme l'attracteur de deux similitudes :
- h de centre 0 définie par
- l de centre 1 définie par .
Notes et références
Notes
- E. Cesaro, Fonctions continues sans dérivée, Archiv der Math. und Phys. 10 (1906) p. 57-63
- G. Farber, Über stetige Funktionen II, Mathematische Annalen, 69 (1910) p. 372-443.
- Paul Lévy, Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole (1938), reprinted in Classics on Fractals Gerald A. Edgar ed. (1993) Addison–Wesley, (ISBN 0-201-58701-7)
- Duvall, P. and Keesling, J., The Hausdorff Dimension of the Boundary of the Lévy Dragon, 22 jul 1999
- Le pavage du plan par la courbe de Lévy, Dubuc Serge & Li Jun
- On 2-reptiles in the plane, Ngai, 1999
- Robert Ferreol, « mathcurve »
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lévy C curve » (voir la liste des auteurs).
- (en) S. Bailey, T. Kim, R. S. Strichartz, « Inside the Lévy dragon », American Mathematical Monthly, vol. 109, no 8, , p. 689–703



