Constante parabolique universelle
La constante parabolique universelle est une constante mathématique.
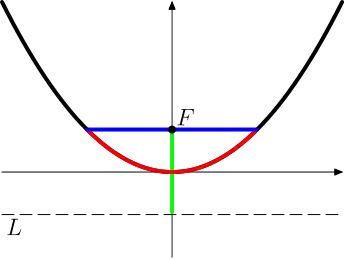
La constante parabolique universelle est la longueur rouge divisée par la demi longueur bleue (ou la longueur verte).
Elle est définie comme le rapport, noté P, pour toute parabole, de la longueur de l'arc de la parabole délimité par la corde focale, par la demi-longueur de cette corde, le paramètre  de la conique. Pour une parabole, le paramètre est aussi égal à la distance du foyer à la directrice, notée L dans la figure ci-contre.
de la conique. Pour une parabole, le paramètre est aussi égal à la distance du foyer à la directrice, notée L dans la figure ci-contre.
La valeur de la constante parabolique est donnée par :

(suite A103710 de l'OEIS).
Démonstration
Soit  l'équation de la parabole ; alors
l'équation de la parabole ; alors

Propriété
P est un nombre transcendant.
- Preuve. Supposons que P soit algébrique. Alors
 serait algébrique. Cependant, par le théorème d'hermite-Lindemann,
serait algébrique. Cependant, par le théorème d'hermite-Lindemann,  serait transcendant, ce qui est faux. Donc P est transcendant.
serait transcendant, ce qui est faux. Donc P est transcendant.
On en déduit que P est irrationnel.
Cas d'une conique quelconque
Pour un cercle, le rapport analogue est égal à sa demi-longueur divisée par son rayon, soit le nombre  .
.
Pour une conique d'excentricité e, le rapport analogue est égal à  où
où  , conduisant à une intégrale elliptique. On vérifie que
, conduisant à une intégrale elliptique. On vérifie que  et
et  .
.
Autre apparition de cette constante
La distance moyenne d'un point choisi au hasard dans un carré de côté 2a à son centre est

- Preuve.

Remarque :
- la distance moyenne d'un point choisi au hasard dans un disque de rayon a à son centre est égale à
 .
.
- la distance moyenne entre deux points du carré unité vaut
 , voir la suite A091505 de l'OEIS.
, voir la suite A091505 de l'OEIS.
Références
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.















