Constante MRB

La constante MRB (ou constante de Marvin Ray Burns) est une constante mathématique de premières décimales 0,187859… suite A037077 de l'OEIS. La constante porte le nom de Marvin Ray Burns qui l'a découverte, et a publié sa découverte en 1999[1]. Burns a initialement nommé cette constante "rc" pour root constant[2] (constante de la racine en français) mais, sur la suggestion de Simon Plouffe, la constante a été renommée[3].

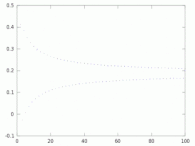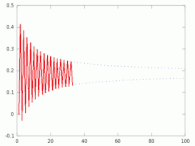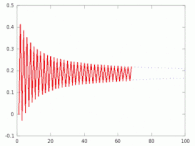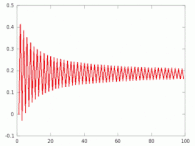
La constante MRB est définie comme la limite supérieure de la somme partielle[4] - [5]

${\displaystyle s_{n}=\sum _{k=1}^{n}(-1)^{k}{\sqrt[{k}]{k}}}$

Quand ${\displaystyle n}$ tend vers l'infini, cette somme a pour limites inférieure et supérieure −0,812140… et 0,187859…, séparées par un segment de longueur 1. La constante peut aussi être explicitée comme somme de série semi-convergente :

${\displaystyle 0,187859\ldots =\sum _{k=1}^{\infty }(-1)^{k}({\sqrt[{k}]{k}}-1)=\sum _{k=1}^{\infty }\left({\sqrt[{2k}]{2k}}-{\sqrt[{2k-1}]{2k-1}}\right).}$

Il n'y a pas d'expression de forme fermée de la constante MRB[6], et on ne sait rien de l'algébricité, de la transcendance, ni même de l'irrationalité de la constante MRB.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.