Cercle de Tucker

Il existe trois façons équivalentes de construire un cercle de Tucker.

Par homothétie

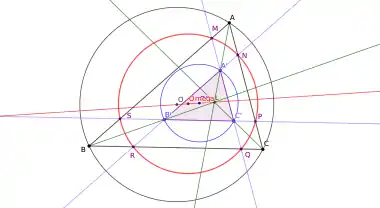
Dans une homothétie de centre le point de Lemoine L, de rapport k (différent de 1 et de 0), le triangle ABC a pour image A’B’C’. Les côtés prolongés du triangle A’B’C’ rencontrent alors ceux de ABC en six points.

Ces points sont sur un même cercle dit cercle de Tucker, et forment un hexagone de Tucker.

Le centre ${\displaystyle \Omega }$ du cercle est le milieu du segment joignant les centres des cercles circonscrits aux deux triangles[3].

Par construction des antiparallèles

On considère un point M du côté [AB], différent de A et B. En traçant l'antiparallèle à (BC) par rapport à (AB) et (AC) passant par M (soit la droite passant par M et parallèle à la tangente au cercle circonscrit de ABC en A), cette droite intersecte AC en un point N. La parallèle à (AB) passant par N intersecte (AC) en un point R. En continuant le processus, ou en traçant directement le cercle passant par M, N et R, on construit les trois points S, P et Q qui complètent l'hexagone de Tucker.

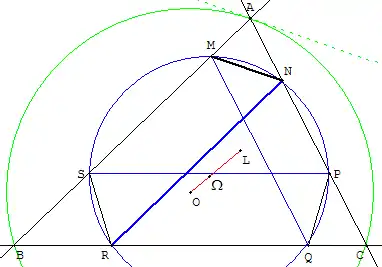
En effet, un raisonnement sur les antiparallélismes permet de vérifier que (PQ) est antiparallèle de (AC) par rapport à (BA,BC)

Par construction de trois antiparallèles de longueur égale

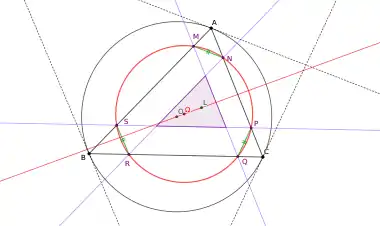
Les droites (MN), (PQ) et (RS) sont antiparallèles aux côtés du triangle et les segments qu'elles déterminent sont de même longueur.

Cette propriété peut être prise comme définition en déterminant trois segments [MN], [PQ], [RS] de longueur égale et parallèles aux tangentes en A, B, C au cercle circonscrit.

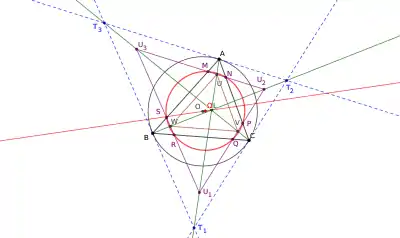
En revenant de la construction par homothétie du cercle de Tucker pour la définition des points U, V, W. On définit les points U₁, U₂ et U₃, intersections des droites (PQ), (RS) et (MN). Ils sont situés sur les symédianes. Le triangle U₁U₂U₃ est le triangle tangentiel de UVW, et est homothétique du triangle tangentiel T₁T₂T₃ de ABC dans l'homothétie de centre L.

Les milieux forment un triangle UVW se déduisant de ABC dans une homothétie de centre L de rapport k. Dans cette homothétie, le point O a pour image Ω avec LΩ/LO = |k|. Ce point Ω est le centre du cercle circonscrit à UVW. La droite (UΩ) parallèle à (OA) est perpendiculaire à (MN), c'est la médiatrice de [MN]. De même (VΩ) est la médiatrice de [PQ]. Ω est bien le centre du cercle (T).

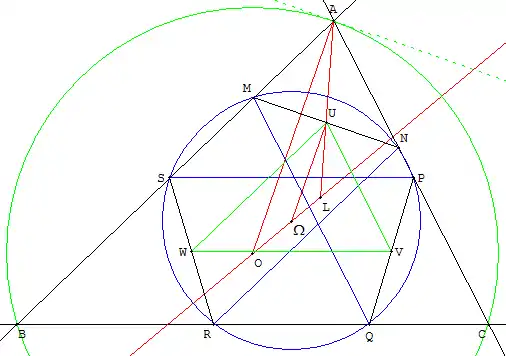
Un cercle de Tucker est caractérisé par son centre Ω situé sur (OL), distinct de O et de L.

Les milieux des côtés de l'hexagone de tucker intérieurs au triangle sont situés sur les symédianes et forment un triangle UVW homothétique de ABC dans une homothétie de centre L.

Les côtés de l'hexagone de Tucker intérieurs au triangle sont antiparallèles aux côtés du triangle et les segments qu'elles déterminent sont de même longueur.

Le centre du cercle de Tucker est le milieu du segment formé par les centres des cercles circonscrits aux triangles ABC et A’B’C’.

En notant le rapport d'homothétie

${\displaystyle k={\frac {L\Omega }{LO}}={\frac {LU}{LA}}={\frac {LV}{LC}}={\frac {LW}{LB}}}$

le rayon du cercle de Tucker vaut

${\displaystyle R_{T}=R{\sqrt {k^{2}+(1-k)^{2}\tan ^{2}\omega }}}$

où R est le rayon du cercle circonscrit à ABC et ω son angle de Brocard.

Cas particuliers

On peut en déduire ainsi plusieurs cas particuliers de cercles de Tucker pour un triangle :

• son cercle d'Apollonius (le cercle tangent intérieurement aux trois cercles exinscrits à ABC, pour ${\displaystyle k={\frac {p(p^{2}-r^{2})}{abc}}}$, avec r le rayon du cercle inscrit dans ABC et p son demi-périmètre)
• son cercle circonscrit (pour k = 1)
• ses deux cercles de Lemoine (pour k = 1/2 et k = 0, respectivement)
• son cercle de Taylor (pour ${\displaystyle k=-\cos {\hat {A}}\cos {\hat {B}}\cos {\hat {C}}}$)
• ses cercles de Gallatly et de Kenmotu

• T. Lalesco, Géométrie du triangle, Vuibert, 1952, chapitre7
• Yvonne et René Sortais, La géométrie du triangle, Hermann 1997, pages 168 à 173 (ISBN 978-2-7056-1429-4)
• Jacques Bouteloup, Cercles de Tücker, Quadrature n°63, Janvier-Mars2007, pages 28 à 32

• François Lobit, Propriétés géométriques exceptionnelles du triangle, Publibook, 2015, pages 30,31

• Patrice Debart, Géométrie du triangle,
• (en) Eric W. Weisstein, « Tucker circles », sur MathWorld.