Carré de Polybe
Le carré de Polybe est une technique de chiffrement par substitution monoalphabétique ancienne, décrite pour la première fois vers 150 av. J.-C. par l'historien grec éponyme[1]. Celle-ci a été utilisée par plusieurs civilisations de différentes manières tout au long de l’histoire[2] - [3] - [4] - [5].
Principe

Le principe est assez simple, il consiste à ordonner les lettres de l’alphabet en ordre alphabétique dans un tableau carré de 5 cases de côté dont chaque ligne et chaque colonne sont numérotées, de gauche à droite et de haut en bas. Considérant que l’alphabet français comporte 26 lettres et que le carré possède seulement 25 cases, par convention les lettres i et j sont fusionnées — comme dans l’image ci-contre. Parfois, d’autres lettres sont fusionnées à la place de celles-ci comme x et z ou encore c et k.

Ensuite, pour chiffrer un mot, il faut trouver la paire de numéros correspondants à chaque lettre. Le premier chiffre est le numéro de la ligne et le second celui de la colonne. Par exemple, le mot « bonjour » est ainsi chiffré par le carré de Polybe : 12 34 33 24 34 45 42 (c'est le codage classique, mais il existe des variantes décrites ci-dessous). Pour déchiffrer un mot, il suffit d'effectuer la méthode inverse[2] - [4] - [5] - [6].
Avantages
Grâce à sa simplicité, la majorité des gens sont capables de chiffrer un message sans aide [2]. Les lettres sont converties en chiffres puisqu’elles sont représentées par deux chiffres faisant partie de l’ensemble {1, 2, 3, 4, 5}[6]. On représente donc 26 lettres avec seulement 5 symboles. Ce procédé est appelé le fractionnement[7].
Limites
De base, le carré de Polybe utilise toujours la même clé — l’ordre des lettres dans le tableau reste toujours identique. Il est donc facilement déchiffrable par une analyse fréquentielle puisque celui-ci est un chiffrement par substitution monoalphabétique[7] - [8].
De plus, la forme la plus simple du carré de Polybe ne contient pas de chiffres ni de caractères spéciaux tels que l’espace, le point, les accents, etc. Il faut savoir qu'une phrase contenant des chiffres ou des symboles ne peut être chiffrée, sans quoi cela peut causer de l’incompréhension lors du déchiffrement. Le fait de fusionner la lettre i et j peut causer une certaine déformation du message original[7] tout comme la suppression des espaces. À titre d'exemple, en anglais « NOW IN » peut également être « NO WIN » selon l’emplacement de l’espace[7].
Utilisations
Le carré de Polybe a été utilisé, entre autres, pour aider la télégraphie mais également pour transmettre un message entre des bateaux sur de longues distances. Son usage se justifiait par la nécessité de transmettre un maximum d’informations avec un minimum d’objets. Plusieurs méthodes de transmissions se basent sur ce principe, dont les trois suivantes[2] - [8] :
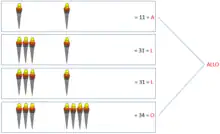
La première utilise des torches : le nombre de torches à gauche étant le numéro de la ligne et le nombre de torches à droite le numéro de la colonne dans le carré de Polybe. L’avantage de cette méthode est que l’on utilise au maximum 10 objets qui peuvent être identiques[3].
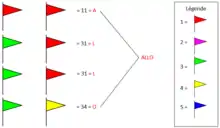
La deuxième méthode de transmission s’aide de drapeaux de cinq couleurs différentes représentant les chiffres de 1 à 5. Celui de gauche représentant le numéro de la ligne et celui de droite le numéro de la colonne. Cette méthode a pour avantage de ne nécessiter l’utilisation que de 5 objets distincts et au maximum deux simultanément. Par contre, il était obligatoire d’avoir décidé la représentation de chaque couleur du drapeau au préalable[8].
La troisième méthode fut utilisée en donnant des coups sur les murs et les tuyaux de prisons. Plusieurs prisonniers américains de la Guerre du Viêt Nam communiquaient entre eux sans que personne s’en aperçoive en cognant sur les murs et les tuyaux de leur cellule. La première série de coups pour le numéro de la ligne et la seconde pour le numéro de la colonne suivi d’un silence[2] - [3] - [5] - [8].
Finalement, les trois méthodes ressemblent à des versions simplifiées du code Morse qui est, par ailleurs, plus facile d’apprentissage[2] - [8].
Variantes
Considérant que le carré de Polybe possède plusieurs limitations et qu'il a été créé il y a longtemps, des variantes y ont été apportées dans le but de l'améliorer. En voici quelques-unes.
Avec une clé

Le moyen le plus simple pour renforcer la méthode de chiffrement est sans aucun doute d'ajouter une clé. Le principe est qu’une fois la clé choisie, il suffit d’ajouter chacune de ses lettres sans répétition au début du carré de Polybe. Ensuite, il faut ajouter les autres lettres de l’alphabet en ordre alphabétique. Par exemple, le carré de Polybe avec la clé WIKIPÉDIA est représenté par l'image ci-contre. L’ajout d’une clé pour augmenter la robustesse peut également être effectué pour chacune des variantes du carré de Polybe[2] - [5].
Avec des chiffres

L’une des variantes consiste à agrandir le carré à 36 cases — soit 6 lignes et 6 colonnes — pour y inclure les chiffres de 0 à 9 à la fin et d’y séparer les lettres i et j, ce qui élimine la confusion lors du déchiffrement du message[2] - [8].
Avec des chiffres et des symboles
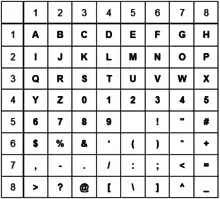
L’une des plus importantes variantes du carré est celle comportant 64 cases — soit 8 lignes et 8 colonnes — pour y inclure lettres, chiffres et autres symboles. Les lettres sont en ordre alphabétique, les chiffres sont en ordre ascendant allant de 0 à 9 et les autres symboles sont en ordre de leur apparition sur la table ASCII. Avec cette variante, il est désormais possible de chiffrer plusieurs messages contenant des adresses courriel, des dates de différents formats, des symboles spéciaux, des phrases avec espaces, etc. Cette variante, tout comme celle qui ajoute les chiffres, permet de séparer les lettres i et j pour éliminer la confusion lors du déchiffrement du message[7].
Avec permutation des chiffres


La première méthode de lectures permutées est relativement simple. Au lieu de lire la paire de chiffres représentant une lettre par le numéro de la ligne suivi du numéro de la colonne, il faut la lire en permutant le numéro de la colonne et le numéro de la ligne à chaque fois ce qui donne le numéro de la colonne suivi du numéro de la ligne[8].
La seconde méthode est plus complexe puisqu'elle consiste à chiffrer le message avec une alternance de la permutation des chiffres. Si la position de la lettre dans le message est paire, elle est chiffrée par le numéro de la colonne suivi du numéro de la ligne. À l'inverse, si la position de la lettre dans le message est impaire, elle est chiffrée par le numéro de la ligne suivi du numéro de la colonne. Tel que montré dans l'exemple, cette méthode permet de chiffrer la même lettre différemment, ainsi la lettre O est chiffrée par 43 et 34. Ce procédé a pour effet de rendre l’analyse fréquentielle plus difficile[7] - [8].
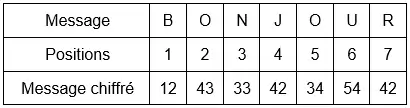
Position paire : (Colonne-Ligne).
Position impaire : (Ligne-Colonne).
Travaux dérivés
Même si le carré de Polybe n’est pas à l’origine une méthode permettant un chiffrement fort, elle a servi de base pour plusieurs autres systèmes de chiffrement plus modernes et rendant plus difficile la cryptanalyse. Le chiffre de Delastelle, le chiffre ADFGVX et le chiffre de nihiliste font partie de ces travaux dérivés[4] - [5] - [6] - [7].
Notes et références
- Cf. Polybe (trad. du grec ancien par D. Roussel), Histoire, vol. X, Paris, Gallimard, coll. « Quarto », , 1503 p. (ISBN 978-2-07-073539-6 et 2-07-073539-7), « 7, §43-47 », p. 748.
- (en) Daniel Rodriguez-Clark, « Cryptography Worksheet — Polybius Square » [PDF], sur Crypto Corner (consulté le ), p. 1-3.
- Cf. Quentin Stiévenart, « La cryptologie. Peut-on réellement cacher des informations ? » [PDF] (consulté le ), p. 4 et p. 12-13.
- Cf. Omary Fouzia, « Applications des algorithmes évolutionnistes à la cryptographie (thèse) » (consulté le ), p. 25-26.
- (en) David Salomon, Data privacy and security, Springer, , 454 p. (ISBN 978-1-280-18956-2, lire en ligne), p. 28-30, p. 50 et p. 88-89.
- (en) PUBLIC KEY CRYPTOSYSTEMS: HISTORY AND DEVELOPMENT (consulté le 29 octobre 2015), p. 12-14 et p. 234-237.
- (en) An Extended Version of the Polybius Cipher[PDF] (consulté le 29 octobre 2015), p. 30-33.
- (en) Polybius Square[PDF] (consulté le 29 octobre 2015), p. 25-26.