Boîte d'Edgeworth

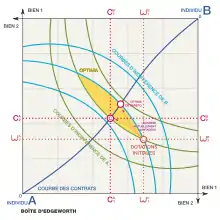
La boite d'Edgeworth, associée aux courbes d’indifférence (ou d'iso-utilité), permet une représentation géométrique simple de la notion d'équilibre pour une économie composée de deux agents, A et B, et de deux types de biens, 1 et 2. Selon ce modèle chaque agent est capable de classifier l'espace des biens (commodités) par une famille de courbe de même utilité (courbes d'indifférence). Par hypothèse, ces courbes sont convexes et plus elles sont éloignées de l'origine plus la préférence est grande pour l'agent. Dans ce modèle les optima de Pareto sont représentés par la courbe des contrats, les points de l'espace des biens où les courbes d'indifférence de l'agent A sont tangentes à celles de l'agent B. Étant donné une situation initiale autre qu'un optimum de Pareto il existe toute une zone d'échange favorable, i.e. qui augmente la préférence des deux agents et dans cette zone une famille d'optima de Pareto, points où il n'est pas possible d'augmenter la préférence d'un agent sans diminuer celle de l'autre.

Boîte d'Edgeworth et courbe de contrat

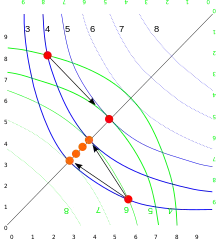
On peut représenter les préférences d'un individu en utilisant les courbes d'indifférence. En prenant l'origine en bas et à gauche on a tracé en bleu plusieurs courbes d'indifférence correspondant à différents niveaux d'utilité. L'individu 1 possède 2 unités du premier bien (en abscisse) et 8 unités du deuxième bien (en ordonnée). Le point rouge en haut et à gauche correspond au stock de biens du premier individu.

On peut faire la même chose pour un deuxième individu mais en renversant le graphique de telle sorte que son origine est en haut et à droite. Les courbes d'indifférence en vert apparaissent concaves depuis l'origine du premier individu.

Le deuxième individu possède 8 unités du premier bien et 2 unités du deuxième. On emboîte maintenant le graphique renversé du deuxième individu contre celui du premier. La grandeur de la boîte sera ainsi de 10 unités du premier bien et de 10 unités du deuxième bien. Le point rouge en haut et à gauche représente le stock de biens des deux individus (la quantité des biens du deuxième est mesurée de droite à gauche et de haut en bas).

Les deux individus sont prêts à échanger les biens afin d'obtenir une quantité préférée. Ils réalisent qu'ils ont intérêt à choisir des quantités où les courbes d'indifférence sont tangentes. En effet, dans les autres cas (lorsque le point représentant les stocks respectifs des agents n'appartient pas à la courbe de contrat) il est impossible d'augmenter la satisfaction d'un individu sans diminuer celle de l'autre. Autrement dit, chaque point de la courbe de contrat constitue un optimum de Pareto.

L'ensemble des points de tangence est appelé la courbe de contrat car un contrat entre les deux concernera un point sur cette courbe. Si les courbes d’indifférence ne sont pas convexes, la courbe de contrat peut prendre des formes très spéciales[3].

Comme chaque individu accepte un échange uniquement s'il préfère le nouveau stock à l'ancien, la solution choisie sur la courbe de contrat sera délimitée par les courbes d'indifférence qui passent par le stock. Selon la terminologie de la théorie des jeux coopératifs, les points entre ces deux limites constituent le noyau ou le cœur de l'économie d'échange. On a représenté un cas (en rouge) lorsque le stock est en haut et à gauche et plusieurs points lorsque le stock est en bas (5.8 unités du premier bien et 1.5 unité du deuxième pour le premier individu, 4.2 unités du premier bien et 8.5 unités du deuxième bien pour le deuxième individu).

En cas de concurrence parfaite, les individus sont confrontés au même rapport de prix et l’équilibre est dans le noyau. Dans ce cas le noyau se réduit et coïncide à l’équilibre de concurrence parfaite[4].

Le noyau peut être vide (ne pas exister) dans des cas très spéciaux[5].

• C. Abraham et A. Thomas, Microéconomie: décisions optimales dans l’entreprise et dans la nation, Dunod, 1970
• John Creedy, Edgeworth and the Development of Neoclassical Economics, Basil Blackwell, Oxford, 1986
• W. Hildenbrand and A.P. Kirman, Introduction to Equilibrium Analysis, North-Holland, 1976
• Peter Newman, The Theory of Exchange, Prentice-Hall, 1964
• Hal R. Varian, Intermediate Microeconomics, a Modern Approach, Norton, 2009