Barres d'Hopkinson

Schéma de la barre de pression développée par Bertram Hopkinson en 1914.

Les barres d'Hopkinson ont été suggérées pour la première fois par l'ingénieur britannique Bertram Hopkinson en 1914[1] comme un dispositif de mesure de la propagation d'un pulse de pression dans une barre métallique. Plus tard, en 1949, H. Kolsky[2] affine la technique d'Hopkinson en utilisant deux barres en série, maintenant connues sous le nom de barres d'Hopkinson divisées. Plus tard, des modifications ont permis les essais de traction, de compression et de torsion. En 2014, la Royal Society fête le centenaire de l'article présentant les barres d'Hopkinson[1] en publiant des articles en rapport[3].

La déformation d'un matériau induite par un choc dans une structure (par exemple à l’extrémité d’une barre) ne se déplace pas instantanément, mais se propage sous forme d’une Onde, comme les ronds produits par un caillou jeté dans l’eau. À noter que la déformation est accompagnée d'une contrainte Contrainte (mécanique) et d'une vitesse, les trois étant liées entre elles.

Dans une barre dont la géométrie est simple, il est assez facile de modéliser ce phénomène. Beltram Hopkinson a le premier utilisé une barre pour étudier l’impact d’une balle de fusil sur une cible[4]. Le modèle de propagation permet de déduire, à partir d’une mesure de l’onde en un point de la barre, la valeur de cette onde en tout point de la barre. Dans les systèmes modernes, dont la configuration de base est due à Kolsky, on place l’échantillon entre deux barres, la barre entrante et la barre sortante (fig. 1). L’essai consiste à frapper la barre entrante par un impacteur.

Le choc induit dans la barre entrante une onde incidente qui se propage vers l’échantillon. Lorsqu’elle l’atteint, elle est réfléchie dans la barre entrante et transmise dans la barre sortante. Des jauges de déformation placées sur les barres permettent de mesurer la déformation associée à ces trois ondes (fig. 2).

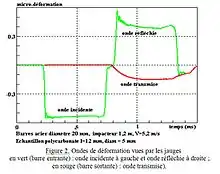
Partant des ondes vues par les jauges, le modèle de propagation déduit la valeur des ondes au niveau de l’échantillon. Cette opération est appelée le transport du signal. Le transport consiste à calculer 1) la forme de l’onde incidente à son arrivée sur l’échantillon, c’est-à-dire un temps après son passage à la position de la jauge et 2) la forme de l’onde réfléchie et de l’onde transmise au départ de l’échantillon, c’est-à-dire un temps avant leur passage à la position de la jauge. La connaissance des ondes sur chaque face de l’échantillon permet ensuite de calculer les forces et les déplacements auxquels il est soumis et donc d’estimer la relation entre son raccourcissement et la force de compression qu’il subit. En supposant l’échantillon assez petit pour justifier deux hypothèses : 1) l’égalité des forces qui lui sont appliquées et 2) l’homogénéité de la déformation, et dans le cas où les barres sont de même nature (même matériau, même diamètre), la contrainte et la déformation uniaxiales de l’échantillon en fonction du temps sont données par les formules suivantes, dues à Kolsky :

Le choix de cette configuration était essentiel à l’époque de Kolsky car elle permettait, avec des barres de même longueur et les jauges au milieu de chaque barre, une analyse de l’essai à partir d’un oscilloscope « à mémoire de trace »[5]. Ces formules, simples, ont largement contribué au succès de la méthode mais elles ont aussi freiné son évolution, car elles s’appliquent à une configuration spécifique.

Les principales limites de la méthode ont été repoussées grâce aux techniques numériques modernes[6] :

• il n’est plus nécessaire aujourd’hui d’utiliser des barres identiques ;
• le transport, fondé sur des résultats théoriques anciens, est réalisé de manière plus précise grâce à la prise en compte d’un modèle de propagation plus fin décrivant la dispersion des ondes[7] - [8] - [9]
• on sait corriger l'effet de poinçonnement local en bout de barre[10] ;
• la durée de la mesure n'est désormais plus limitée par la superposition des ondes[11]