Axe optique
L’axe optique d'un système optique centré, ou axe principal, est l'axe de symétrie de rotation du système.
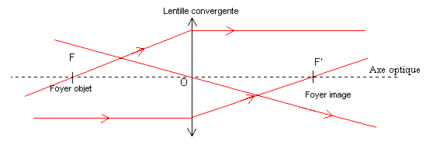
Définition
Le concept d'axe optique n'a de raison d'être que dans un système dit « centré », c'est-à-dire dans lequel les différents éléments sont à symétrie de révolution[1] - [2], même s'ils ne sont pas sphériques. Ainsi tant qu'une lentille asphérique à symétrie de révolution n'est pas hors d'axe, on peut considérer le système comme de révolution et l'axe optique existe[3] - [4].
Pour les miroirs on définit la plupart du temps l'axe optique comme la droite reliant le sommet du miroir et son centre de courbure. Un rayon passant par le centre et le sommet sera réfléchit vers le centre[5]. Dès lors que la symétrie de révolution est conservée, il est possible de parler d'axe optique d'un système, catoptrique, dioptrique ou catadioptrique[6], il est par ailleurs possible d'analyser un système hors d'axe contenant des réflexions en considérant le « système déplié » équivalent, ramenant la combinaison à un système de révolution[7].
Plus simplement, l'axe optique est l'axe contenant tous les centres de courbures des surfaces du système[8].
Tracé de rayons
L'axe optique est généralement orienté de gauche à droite, et dans un repère orthonormé, il est l'axe (Oz)[6], son sens indiquant la direction de propagation de la lumière[9], il représente en fait le tracé d'un rayon lumineux passant par le centre du système et n'étant pas dévié lors de la traversée dans le cas d'un système centré[2]. De plus tout point objet situé sur l'axe est imagé sur l'axe et les foyers du système sont positionnés sur l'axe optique.
Dans le cadre de l'approximation de Gauss, les rayons sont considérés comme étant proches et peu inclinés par rapport à l'axe optique[2] et sont nommés « rayons paraxiaux »[10] d'où le nom d'« optique paraxiale » désignant le domaine de l'optique géométrique couvert par l'approximation de Gauss.
L'axe optique permet de définir par ailleurs les plans méridiens, plans contenant cet axe, et les « rayons méridiens », contenus dans ces plans par opposition aux « rayons obliques »[n 1] ; les rayons lumineux passant par un point objet appartenant à l'axe optique sont des « rayons axiaux »[11] - [10].
Outre les types de rayons d'un système, d'autres éléments sont définis par l'axe optique, notamment la pupille d'entrée et la pupille de sortie de la combinaison, placées respectivement à l'intersection de la droite portant le rayon principal dans l'espace objet avec l'axe optique, et à l'intersection de la droite portant le rayon principal dans l'espace image avec l'axe optique ; le rayon principal étant le rayon passant par le centre du diaphragme de la combinaison optique[12].
Aberrations
Il est possible de classer les aberrations optiques de multiples manières, dont en les séparant entre aberrations hors d'axe et aberrations sur l'axe[13]. Certaines aberrations existent effectivement exclusivement dans tous les points de l'espace image sauf l'axe optique : elles sont hors d'axe. Les autres sont des aberrations existant dans tout l'espace, dont l'axe optique. Sur l'axe, on retrouvera ainsi l'aberration sphérique et le chromatisme axial[14] - [13]. Les autres aberrations ont un comportement faisant que plus on prend un point éloigné de l'axe, plus elles sont importantes[8].
Autres systèmes
Pour une fibre optique, l'axe optique ou axe de la fibre suit le centre du cœur de la fibre et n'est donc pas obligatoirement une droite. Cette définition s'applique de manière générale à tous les guides d'ondes optiques[15]. L'axe optique étant un invariant pratique dans un système il permet aussi de définir les gradients d'indice : selon l'axe optique le gradient est dénommé gradient axial, et s'il est perpendiculaire à l'axe, un gradient radial[16].
Notes et références
Références
- Balland 2007, p. 102
- H Prépa, première année, p.50
- Balland 2007, p. 344
- Malacara-Hernández et Malacara-Hernández 2013, p. 11
- Balland 2007, p. 214
- Handbook of optics, v.I, p.1.35
- Handbook of optics, v.I, p.1.36
- Malacara-Hernández et Malacara-Hernández 2013, p. 117
- Balland 2007, p. 197
- Malacara-Hernández et Malacara-Hernández 2013, p. 12
- Handbook of optics, v.I, p.1.39
- Malacara-Hernández et Malacara-Hernández 2013, p. 23
- Riedl 2001, p. 37
- Malacara-Hernández et Malacara-Hernández 2013, p. 95
- Optical waveguide communications glossary 1985, p. 41
- Malacara-Hernández et Malacara-Hernández 2013, p. 7
Notes
- En anglais on parlera de skew rays ou de oblique rays.
Bibliographie
- Optique 1re année MPSI-PCSI-PTSI, Hachette Éducation Technique, coll. « H Prépa », , 224 p.
- Bernard Balland, Optique géométrique : Imagerie et instruments, Presses polytechniques et universitaires romandes, , 860 p.
- (en) Handbook of optics : Fundamentals, techniques & design, vol. I, New York/San Francisco/Washington etc., McGraw-Hill, , 2e éd., 1628 p. (ISBN 0-07-047740-X)
- (en) Daniel Malacara-Hernández et Zacarías Malacara-Hernández, Handbook of Optical Design, CRC Press, , 3e éd., 585 p. (lire en ligne)
- (en) Max J. Riedl, Optical design fundamentals for infrared systems, SPIE Press, , 2e éd., 182 p. (ISBN 0-8194-4051-5, présentation en ligne)
- (en) Optical Waveguide Communications Glossary, Boulder, U. S. Department of Commerce, , 67 p. (lire en ligne)