Arbre palindromique

L'arbre palindrome pour un mot ${\displaystyle S}$ de longueur ${\displaystyle n}$ est une structure de donnée sous forme d'un graphe proche d'un arbre et qui représentent tous les palindromes distincts qui sont facteurs de ${\displaystyle S}$ avec une place additionnelle en ${\displaystyle O(n)}$[2]. Lorsque ${\displaystyle S}$ est de longueur ${\displaystyle n}$ sur un alphabet de taille ${\displaystyle \sigma }$ et est donnée on-line, l'arbre peut être construit en temps ${\displaystyle O(n\log \sigma )}$ et place ${\displaystyle O(n)}$.

Les sommets du graphe représentent des palindromes, les arcs décrivent le passage d'un palindrome au suivant ou à un précédent.

Il y a deux types d'arcs, des arcs directs — qui sont les arcs d'un arbre — et des liens suffixes qui permettent de revenir en arrière.

Les arcs directs sont étiquetés par des symboles de l'alphabet. Il y a un arc direct du sommet ${\displaystyle u}$ vers le sommet ${\displaystyle v}$ étiqueté par la lettre ${\displaystyle a}$ si ${\displaystyle v=aua}$ :

${\displaystyle u\xrightarrow {a} v\iff v=aua}$.

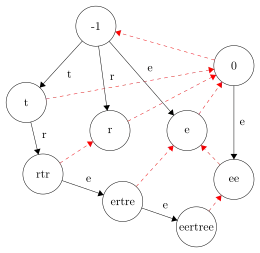
Ainsi, on a dans l'exemple, les arcs

${\displaystyle {\mathsf {t}}\xrightarrow {\mathsf {r}} {\mathsf {rtr}}\xrightarrow {\mathsf {e}} {\mathsf {ertre}}\xrightarrow {\mathsf {e}} {\mathsf {eertree}}}$.

Les liens suffixes sont des arcs qui vont d'un sommet ${\displaystyle u}$ au sommet ${\displaystyle v}$, où ${\displaystyle v}$ est le plus long suffixe palindrome propre de ${\displaystyle u}$. Dans l'exemple, les liens suffixes sont tracés en rouge. On a par exemple :

${\displaystyle {\mathsf {eertree}}\ {\color {Red}\to }\ {\mathsf {ee}}\ {\color {Red}\to }\ {\mathsf {e}}\ {\color {Red}\to }\ 0}$.

Deux sommets spéciaux sont ajoutés à la structure :

• le sommet ${\displaystyle -1}$ qui est la racine de l'arbre ; les arcs sortant de ce sommet et étiqueté ${\displaystyle a}$ ont pour extrémité le sommet ${\displaystyle a}$ ; on a donc, pour tout symbole figurant dans ${\displaystyle S}$, l'arc

${\displaystyle -1\xrightarrow {a} a}$.

• Le sommet ${\displaystyle 0}$ qui représente le mot vide (qui est un palindrome) ; on a alors

${\displaystyle 0\xrightarrow {a} aa}$

si ${\displaystyle aa}$ est facteur de ${\displaystyle S}$. Le sommet ${\displaystyle 0}$ est le lien suffixe du sommet ${\displaystyle -1}$ et de lui-même.

La notation curieuse pour ces sommets particuliers est une conséquence de la numérotation des sommets de l'arbre, qui va de 1 jusqu'à un entier qui est aussi le nombre de palindromes figurant dans le mot ${\displaystyle S}$.

On peut montrer[2] que la construction de l'arbre palindromique peur se faire en temps ${\displaystyle O(n\log \sigma )}$ et place ${\displaystyle O(n)}$. Des variantes ont été données notamment par Mieno, Watanabe et al.[3].

• Mikhail Rubinchik et Arseny M. Shur, « EERTREE: An efficient data structure for processing palindromes in strings », Lecture Notes in Computer Science, vol. 9538 « Combinatorial Algorithms. IWOCA 2015 »,‎ 2016, p. 321-333 (DOI 10.1007/978-3-319-29516-9_27, arXiv 1506.04862)
• Mikhail Rubinchik et Arseny M. Shur, « EERTREE: An efficient data structure for processing palindromes in strings », European Journal of Combinatorics, vol. 68,‎ février 2018, p. 249-265 (DOI 10.1016/j.ejc.2017.07.021, arXiv 1506.04862) — version "journal" de l'article précédent
• Takuya Mieno, Kiichi Watanabe, Yuto Nakashima, Shunsuke Inenaga, HideoBannai et MasayukiTakeda, « Palindromic trees for a sliding window and its applications », Information Processing Letters, vol. 173,‎ janvier 2022, article n^o 106174 (DOI 10.1016/j.ipl.2021.106174, lire en ligne )

• « Palindromic tree » ; blog sur adilet.org.
• « Palindromic Tree : Introduction & Implementation » ; sur geeksforgeeks.org.

• Palindrome
• Longueur palindromique d'un mot