Apprentissage par renforcement hors ligne

Problème du Mountain car

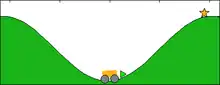
Le Moutain car est un problème classique de la littérature de l'apprentissage par renforcement, dans lequel une voiture doit atteindre le haut d'une colline.

• Les états sont décrits par la position de la voiture (${\displaystyle p\in [-1.2,0.6]}$) et sa vitesse (${\displaystyle s\in [-0.07,0.07]}$);
• Les actions sont les accélérations possibles de la voiture : accélérer vers l'avant, vers arrière, ou rester en roue libre.
• La fonction de transition est obtenue en effectuant la somme des forces qui s'applique à la voiture;
• La fonction de récompense vaut ${\displaystyle hauteur-1}$

État initial

État d'équilibre

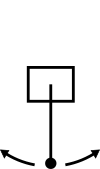
Ce problème est un autre exemple classique, dans lequel un agent doit contrôler une perche munie d'un poids à l'aide d'un moteur pour la placer en équilibre en position verticale, avec le poids en haut. Le moteur n'étant pas assez puissant pour faire passer de la perche de sa position initiale à la position d'équilibre d'un coup, l'agent doit apprendre à faire balancer la perche.

• Les états sont la position de la perche et sa vitesse;
• Trois actions sont possibles : faire tourner le moteur dans les deux sens, ou arrêter le moteur;
• La fonction de transition est inconnue, ses valeurs sont obtenues en observant la perche;
• La fonction de récompense vaut 0 si la perche est à la position d'équilibre (avec une marge de 0.5°) et -1 sinon.

Il existe une grande variété d'algorithmes hors-ligne dans la littérature, mais de manière générale ils brodent tous autour de quelques principes fondamentaux qui les distinguent des algorithmes purement en-ligne ou de ceux dans lesquels le MDP est connu. Initialement pensés pour résoudre les difficultés spécifiques à l'apprentissage hors-ligne, ces principes sont également avantageux dans un cadre plus général.

Pour un Q-learning purement en ligne, l'agent est libre d'explorer et de générer de l'expérience comme bon lui semble. Ces expériences sont utiles par deux aspects:

1. effectivement explorer l'environnement, c'est-à-dire expérimenter de nouvelles transitions vers des états non encore visités et récolter de nouvelles récompenses;

2. faire converger l'algorithme, car celui-ci demande un grand nombre d'itérations pour propager les informations et finalement se stabiliser vers une politique optimale. Dans la situation hors ligne, on ne peut se contenter de n'utiliser qu'une seule fois une expérience donnée car le nombre d'expériences est limité par définition, et ne permettrait pas de faire converger l'algorithme.

Cette difficulté est levée en "rejouant" plusieurs fois les mêmes expériences, c'est-à-dire que le jeu de données disponible est exploité encore et encore comme s'il s'agissait de nouvelles expériences.

Dans les méthodes classiques d'apprentissage par renforcement, il est commun de faire la mise à jour de la fonction de valeur de manière désynchronisée. C'est-à-dire qu'après chaque observation d'une transition, la valeur d'un état ou d'un état-action est mise à jour localement et les autres états sont laissés inchangés. Ensuite, ce n'est que lors de nouvelles interactions que les autres états seront évalués sur la base de la valeur mise à jour précédemment.

Les algorithmes batch, dans le but d'exploiter au maximum les données disponibles, de s'adapter à des espaces d'états continus et de contrer certains problèmes d'instabilités lors de l'apprentissage (cas de non convergence), ne se contentent pas de stocker simplement les valeurs pour chaque état ou action et d'appliquer des mises à jour de type programmation dynamique. Ils ajoutent au-dessus une forme ou une autre de globalisation et de régularisation des mises à jour qui peut se voir comme un apprentissage supervisé des fonctions de valeurs.

Par exemple, dans les algorithmes que nous présentons ci-dessous, on trouve l'utilisation d'un noyau gaussien qui permet de moyenner localement les valeurs, d'une base de fonctions dans laquelle on exprime la fonction de valeurs, ou plus explicitement d'un algorithme d'apprentissage supervisé (réseau de neurones, k-plus-proches-voisins...) pour apprendre la fonction de valeurs.

De cette manière chaque expérience utilisée va permettre de mettre à jour globalement l'ensemble de la fonction de valeurs (des états ou états-actions) sans nécessiter d'attendre que de multiples itérations propagent l'information de manière plus ou moins aléatoire.

L'algorithme Kernel-Based Approximate Dynamic Programming (KADP) suppose qu'un ensemble de transitions observées de façon arbitraire ${\displaystyle (s,a,r,s')\in F}$ est à sa disposition. Il suppose ensuite que l'espace des états est muni d'une distance, à partir de laquelle la notion de moyennage basé sur un noyau Gaussien prend sens. Ce noyau est utilisé pour mettre à jour itérativement la fonction de valeurs ${\displaystyle V}$ en tous les états, à partir du jeu d'échantillons ${\displaystyle F}$. On voit bien ici l'application de l'idée d'experience replay (on utilise répétitivement toutes les données) et celle de fitting puisque le noyau permet à l'ensemble des valeurs d'être mise à jour par chaque transition.

L'algorithme démarre d'une fonction de valeurs des états ${\displaystyle {\hat {V}}_{0}}$ arbitrairement choisie puis chaque itération du KADP consiste en deux phases:

La première phase évalue la mise à jour du processus décisionnel :

${\displaystyle {\hat {Q}}_{a}^{i+1}(\sigma ):=\sum _{(s,a,r,s')\in F_{a}}k(s,\sigma )[r+\gamma {\hat {V}}^{i}(s')]}$

avec ${\displaystyle F_{a}}$ un sous ensemble de ${\displaystyle F}$ qui n'utilise que les actions a.

Cette équation calcule la moyenne pondérée de la mise à jour habituelle: ${\displaystyle r+\gamma {\hat {V}}^{i}(s')}$ avec comme pondération ${\displaystyle k(s,\sigma )}$. Le noyau est choisi de telle sorte que les transitions les plus éloignées aient une moins grande influence que les plus proches.

La seconde phase consiste à calculer les nouvelles valeurs des états selon la politique gloutonne:

${\displaystyle {\hat {V}}^{i+1}(s)=\max _{a\in A}{\hat {Q}}_{a}^{i+1}(s)}$

L'algorithme va donc itérer sur les équations définies au-dessus pour évaluer ${\displaystyle {\hat {V}}^{i}}$ avec ${\displaystyle i=1,2,\dots }$ et espérer converger vers une unique solution ${\displaystyle {\hat {V}}}$.

Le problème du choix du portfolio optimal décrit dans [1] est un cas pratique du KADP. C'est un problème d'investissement financier où l'agent décide d'acheter ou non des actions. Le but étant à la fin de la simulation de maximiser le gain de l'agent.

Sa représentation comme un MDP est la suivante :

• ${\displaystyle s_{t}}$ l'état symbolisant la valeur de l'action à un instant t
• ${\displaystyle a_{t}}$ l'action représentant l'investissement de l'agent dans l'action avec ${\displaystyle A\equiv {0,0.1,0.2,\dots ,1}}$
• La richesse de l'agent au temps t est ${\displaystyle W_{t}}$ et sa richesse au temps t+1 est ${\displaystyle W_{t+1}=(1+a_{t}{\dfrac {s_{t+1}-s_{t}}{s_{t}}})W_{t}}$

L'agent va donc au cours du temps investir (ou pas) dans une action pour maximiser sa richesse avec comme but d'être le plus riche possible à la fin du temps maximum défini. Pour rendre le problème le plus réaliste possible, l'agent adopte un comportement tel qu'il a peur de perdre ses gains autant qu'il a l'envie d'en gagner.

Cet algorithme permet de calculer une approximation de la fonction de valeurs optimale des états-actions ${\displaystyle Q}$ à partir d'un jeu d'échantillons du MDP. Connaissant ${\displaystyle Q}$, il est alors possible de déduire la politique correspondante : ${\displaystyle \pi (s)=\arg \max _{a\in A}Q(s,a)}$. Il repose sur le même principe que l'algorithme d'itération sur la valeur des états-actions, qui consiste à calculer de manière itérative le point fixe de l'équation de Bellman :

${\displaystyle Q^{i+1}(s,a)=\sum _{s'\in S}[R(s,a,s')+\gamma \max _{a'\in A}Q^{i}(s',a')]T(s,a,s')}$

On cherche à calculer ce point fixe à partir d'un jeu d'échantillons ${\displaystyle {\mathcal {F}}}$ (un ensemble de transitions de la forme ${\displaystyle (s,a,r,s')}$). L'algorithme procède de la manière suivante :

1. Il crée une base de données d'apprentissage ${\displaystyle P}$ constituée des couples entrée-sortie ${\displaystyle (s,a)\to r+\gamma \max _{a'\in A}{\hat {Q}}^{i}(s,a)}$ pour chaque transition ${\displaystyle (s,a,r,s')\in {\mathcal {F}}}$. La valeur ainsi calculée pour chaque ${\displaystyle (s,a)}$ est en quelque sorte la «meilleure estimation» que l'on puisse faire de la valeur de ${\displaystyle Q(s,a)}$ dans l'état actuel des connaissances décrit par ${\displaystyle Q^{i}}$.
2. Il en déduit une fonction ${\displaystyle {\hat {Q}}^{i+1}}$ à partir de l'ensemble ${\displaystyle P}$ en utilisant une méthode d'apprentissage supervisé. Cette fonction est donc une approximation de la fonction ${\displaystyle Q^{i+1}}$ obtenue à la i+1^ème itération de l'algorithme d'itération sur la valeur des états-actions.
3. Il incrémente ${\displaystyle i}$ et retourne à la première étape tant qu'une condition d'arrêt n'est pas vérifiée.

Cet algorithme peut-être utilisé avec n'importe quelle méthode d'apprentissage supervisé, en particulier des méthodes non paramétriques, qui ne font aucune hypothèse sur la forme de ${\displaystyle Q}$. Cela permet d'obtenir des approximations précises indépendamment de la taille des espaces d'états et d'actions, y compris dans le cas d'espaces continus.

On peut consulter [2] pour une mise en œuvre dans laquelle la méthode d'apprentissage est une régression régularisée moindres carrés; un réseau de neurones est utilisé dans [3]; enfin une approche basée sur différents types d'arbres de régression est analysée dans [4].

De manière générale, la convergence de l'algorithme n'a été démontrée que pour une certaine classe de méthodes d'apprentissage. Différentes conditions d'arrêt peuvent être utilisées ; en pratique, fixer le nombre d'itérations permet d'assurer la terminaison de l'algorithme, et ce quelle que soit la méthode d'apprentissage utilisée.

Dans [4], plusieurs problèmes ont été utilisés pour évaluer l'algorithme avec différentes méthodes d'apprentissage supervisé, et avec plusieurs types de batch (pure batch et growing batch). Sur ces problèmes, l'algorithme de fitted Q iteration est très performant, en particulier en utilisant des méthodes d'apprentissage non paramétriques (comme la méthode des k plus proches voisins).

Bien adapté à l'apprentissage pûrement hors-ligne, LSPI est une approche reconnue pour exploiter efficacement un jeu de données fixe préexistant ([5] - [6]).

Cet algorithme est une adaptation de l'algorithme d'itération de la politique exprimé sur la fonction ${\displaystyle Q}$ d'états-actions. Il se focalise exclusivement sur l'évaluation de ${\displaystyle Q}$, et la politique n'y est jamais représentée explicitement, mais simplement déduite à la volée, par le choix glouton classique:

${\displaystyle \pi (s)=\arg \max _{a\in A}Q(s,a)}$

Par rapport à PI, LSPI opère deux grands changements :

1. la fonction ${\displaystyle Q}$ est exprimée comme une combinaison linéaire de fonctions ${\displaystyle \phi _{i}}$, ${\displaystyle i=1,\dots ,k}$:

${\displaystyle Q(s,a)=\sum _{i=1}^{k}w_{i}\phi _{i}(s,a).}$

Les fonctions ${\displaystyle \phi _{i}}$ forment donc une base d'un sous-espace ${\displaystyle {\mathcal {Q}}}$ de l'espace des fonctions états-actions, choisie une fois pour toutes au départ. Ainsi en interne, la fonction ${\displaystyle Q}$ est simplement représentée par les ${\displaystyle k}$ coefficients ${\displaystyle w_{i}}$.

Ce modèle possède un avantage: quels que soient le nombre d'états et d'actions, seuls ${\displaystyle k}$ coefficients sont utilisés pour représenter l'ensemble des valeurs de ${\displaystyle Q}$, contre ${\displaystyle |S|\times |A|}$ si l'on utilisait une représentation tabulaire classique. Ceci permet de traiter efficacement des MDP possédant un grand nombre d'états et/ou d'actions. On peut même, dans ce formalisme, considérer des espaces d'états ou d'actions continus.

L'inconvénient, en revanche, est que l'on est maintenant restreint aux fonctions de ${\displaystyle {\mathcal {Q}}}$. Dans l'algorithme PI avec états-valeurs, la phase d'évaluation de la politique ${\displaystyle \pi }$ consiste à déterminer le point fixe ${\displaystyle Q^{\pi }}$ de l'opérateur

${\displaystyle K(Q)(s,a)=\sum _{s'\in S}[R(s,a,s')+\gamma Q(s',\pi (s'))]T(s,a,s'),}$

soit par la résolution d'un système linéaire, soit par calcul itératif sur ${\displaystyle K}$.

Or même si par définition ${\displaystyle Q\in {\mathcal {Q}}}$, on n'a pas en général ${\displaystyle K(Q)\in {\mathcal {Q}}}$. L'idée dans LSPI est alors de projeter (au sens des moindres carrés, d'où le nom de l'algorithme) la mise à jour ${\displaystyle K(Q)}$ sur ${\displaystyle {\mathcal {Q}}}$:

${\displaystyle K'(Q)={\mathcal {P}}_{\mathcal {Q}}^{\perp }(K(Q)),}$

et donc d'obtenir une approximation ${\displaystyle {\hat {Q}}^{\pi }}$ de ${\displaystyle Q^{\pi }}$ qui est stable par la règle de mise à jour suivie de la projection. Dans [7] ce point fixe est obtenu par résolution d'un système linéaire.

L'algorithme général d'itération de la politique, avec projection moindres carrés.

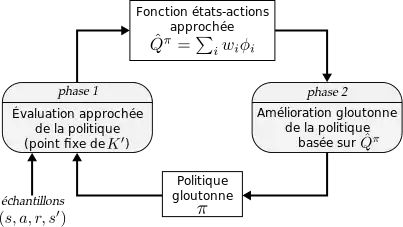
2. La deuxième différence est que LSPI ne suppose pas le MDP connu; l'algorithme se base uniquement sur un jeu d'échantillons du MDP, donnés sous la forme de quadruplets ${\displaystyle (s,a,r,s')}$. Ces échantillons peuvent être donnés directement au départ de l'algorithme (mode pure-batch) ou progressivement (mode semi-batch ou en-ligne). Concrètement, l'algorithme se contente d'effectuer les mises à jour précédentes sur le jeu d'échantillon, éventuellement de façon répétée pour provoquer la convergence («experience replay»). On peut montrer qu'en fait cela revient à appliquer la mise à jour sur le véritable MDP, mais avec les probabilités de transitions ${\displaystyle T(s,a,s')}$ obtenues empiriquement selon la distribution des échantillons. Ainsi, dans l'hypothèse où cette distribution est conforme aux véritables probabilités de transition du MDP sous-jacent, le résultat converge asymptotiquement vers la véritable valeur ${\displaystyle Q^{\pi }}$, et donc finalement vers la fonction optimale ${\displaystyle Q^{*}}$. On peut également remarquer que chaque échantillon contribue linéairement à chaque itération (il ajoute un terme dans la somme définissant ${\displaystyle K}$ et l'opérateur de projection est linéaire), ce qui permet de mettre en place des optimisations lorsque les échantillons arrivent progressivement.

La figure ci-contre résume schématiquement l'algorithme LSPI.

Dans [7], plusieurs applications de l'algorithme LSPI sont proposées. L'une d'elles, dans lequel l'algorithme est particulièrement performant notamment par rapport à un algorithme de Q-Learning, est le problème de l'équilibre et la conduite d'un vélo [8].

Dans ce problème l'apprenant connaît à chaque pas de temps l'angle et la vitesse angulaire du guidon, ainsi que l'angle, la vitesse et accélération angulaire de l'angle que forme le vélo avec la verticale. Il doit alors choisir quelle force rotatoire appliquer au guidon (choisie parmi trois possibilités), ainsi que le déplacement de son centre de masse par rapport au plan du vélo (choisie également parmi 3 possibilités), de manière d'une part à rester en équilibre (c'est-à-dire ici ne pas dépasser un angle vélo/sol de +/- 12°) et d'autre part atteindre une destination cible.

La mise en œuvre est purement hors-ligne et consiste à observer le comportement d'un agent aléatoire pour collecter de l'ordre de quelques dizaines de milliers d'échantillons sous forme de trajectoires. Les trajectoires collectées sont ensuite coupées après quelques pas de temps, pour ne garder que la partie intéressante avant qu'elles ne rentrent dans un scénario de chute inexorable. Les récompenses sont en lien avec la distance atteinte par rapport à l'objectif. Quelques passes de l'algorithme sont ensuite effectuées sur ces échantillons («experience replay») et une convergence très rapide vers des stratégies viables est observée.