Analyse statistique implicative

Fondée dans les années 1980[1] par Régis Gras (1933-2022), professeur émérite à l’université de Nantes, équipe DUKE du Laboratoire d'informatique de Nantes Atlantique, elle continue à se développer sous son impulsion et celle de chercheurs de son équipe, Jean-Claude Régnier[2] entre autres, professeur émérite à Université Lumière Lyon-II et membre de l'UMR 5191 ICAR[3], qui assure la présidence du comité scientifique et de programme des colloques ASI.

Visant l’extraction de règles d’association de nature implicative, la méthodologie consiste à attribuer une valeur numérique, une mesure entre 0 et 1, à des règles R du type ; « si la variable a est observée, alors généralement la variable b l’est aussi » ou dans les cas plus généraux : « si la variable a prend une certaine valeur alors la variable b prend généralement une valeur supérieure ». La mesure attribuée est une probabilité, appelée intensité d’implication. À travers la structuration de l’ensemble des règles, l’utilisateur peut accéder à des relations de type causal et prédictif pondérées par cette intensité. « L'ASI n'est pas une méthode mais un cadre théorique, large, dans lequel se traitent des problèmes modernes de l'extraction des connaissances à partir des données. C'est une théorie générale dans le domaine de la causalité parce qu'elle répond à des faiblesses d'autres théories, elle apporte un outillage formel et des méthodes pratiques de résolution de problèmes. Ses applications sont multiples... » (D. Zighed, professeur des universités au laboratoire ERIC, Université Lumière Lyon-II et ex-Directeur de l'ex Institut des Sciences de l’Homme de Lyon. [Actuellement Maison des Sciences de l'Homme Lyon et Saint-Étienne[4].

Cette probabilité est celle de l’événement aléatoire : « S’il n’existait pas de lien a priori asymétrique entre a et b, le nombre de contre-exemples à la règle R serait, sous le seul effet du hasard, plus grand généralement que le nombre de contre-exemples observés dans la contingence ».

Une modélisation du nombre de contre-exemples aléatoires est choisie et justifiée. Elle permet alors de calculer toutes les mesures attribuées aux couples de variables. Un algorithme conduit à extraire celles correspondant à un seuil fixé par l’expert, par exemple 0.95.

Fig.1 - Graphe implicatif

Fig.2 - Hiérarchie orientée

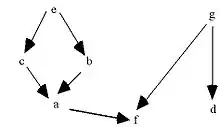
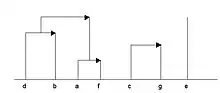
Deux types de représentation permettent de visualiser les relations extraites du corpus donné et en structurent leur ensemble :

• d’une part un graphe pondéré sans cycle où chaque arête représente une règle (fig.1) ;
• d’autre part une hiérarchie ascendante orientée de méta-règles (fig.2).

Si la première représentation présente des affinités avec un treillis de Galois ou à un réseau bayesien, tout en étant basée sur des algorithmes différents plus sensibles aux effectifs des sujets, par contre la deuxième est originale. En effet, les niveaux supérieurs sont des méta-classes non linéaires, comparables à des niveaux de conceptualisation faisant passer du simple au complexe sans inclusion nécessaire (cf. travaux de psychologie cognitive de Jean Piaget ou Lev Vygotsky).

A l’instar des méthodes d’analyse factorielle, (par exemple l’A.F.C. de J.P. Benzecri) des algorithmes sont élaborés pour mesurer la contribution de sujets ou de catégories de sujets aux règles extraites et aux chemins du graphe ou aux classes de la hiérarchie établissant une dualité entre les sujets et les variables.

Un logiciel dénommé C.H.I.C. (acronyme de Classification Hiérarchique Implicative et Cohésitive) est fonctionnel pour traiter tous les problèmes numériques et graphiques nécessaires à l’usage de la méthode A.S.I.. Evolutif suivant les extensions de la théorie, il est développé par Raphaël Couturier, Professeur des universités à l’Université de Franche-Comté. Grâce à cet outil informatique, de nombreuses applications dans des domaines variés (pédagogie, psychologie, sociologie, bio-informatique, médecine, histoire de l’art, etc.) ont montré la pertinence du modèle probabiliste choisi et, de ce fait, la richesse des informations obtenues par le traitement des variables. Elles ont, en particulier, permis de mettre en évidence des pépites de connaissance que d’autres méthodes n’extrayaient pas et d’exprimer des relations causales affectées d’une intensité. Ses avantages tiennent à sa sensibilité aux effectifs des instances et aux représentations aisées à interpréter.

• L'implication statistique. Nouvelle méthode exploratoire de donnée, préface de Edwin Diday, Paris Dauphine et INRIA, sous la direction de R.Gras, et la collaboration de S. Ag Almouloud, M. Bailleul, A. Larher, M. Polo, H. Ratsimba-Rajohn, A.Totohasina, La Pensée Sauvage, Grenoble, 1996.
• Mesures de Qualité pour la fouille de données, H.Briand, M.Sebag, R.Gras er F.Guillet eds, RNTI-E-1, Ed. Cépaduès, 2004
• (en) Quality Measures in Data Mining, F.Guillet et H.Hamilton eds, Springer, 2007.
• (en) Statistical Implicative Analysis, Theory and Applications, préface de Dan A.Simovici, Massachusetts Boston University, R.Gras, E. Suzuki, F. Guillet, F. Spagnolo, eds, Springer, 2008.
• Analyse Statistique implicative. Une méthode d'analyse de données pour la recherche de causalités, préface de Djamel Zighed, Lyon 2, Dir. R. Gras, eds. R. Gras, J.C. Régnier, F. Guillet, Cépaduès Ed. Toulouse, 2009.
• (es) Teoria y Aplicaciones del Analisis Estadistico Implicativo, Eds : P.Orus, L.Zemora, P.Gregori, Universitat Jaume-1, Castellon (Espagne), 2009.
• L'Analyse Statistique Implicative. Méthode exploratoire et confirmatoire à la recherche de causalité, préface de Gilbert Saporta, CNAM, Paris, Dir. R. Gras, eds. R. Gras, J.C. Régnier, C. Marinica, F. Guillet, Cépaduès Ed. Toulouse, 2013.
• Analyse Statistique Implicative. Des Sciences dures aux Sciences Humaines et Sociales. Gras, R., Régnier, JC., Lahanier-Reuter, D. Marinica, C., Guillet, F. (Eds) Cépaduès Ed. Toulouse, 2017.
• La théorie de l'analyse statistique implicative ou l'invraisemblance du faux, Préface de P. Kuntz, Université de Nantes, R. Gras, Cépaduès Ed. Toulouse, 2018.
• Análise Estatística Implicativa e Análise de Similaridade no Quadro Teórico e Metodológico das Pesquisas em Ensino de Ciências e Matemática com a utilização do software CHIC. Régnier, J.C.,Lira Veras Xavier de Andrade, V. (Eds) Brasil. Editora Universitaria da UFRPE. 2023

Depuis 2000, des colloques internationaux avec comité scientifique réunissent près d’une centaine de participants d’une trentaine de pays.

• Colloque ASI 5 à l’université de Palerme en 2010
• Colloque ASI 6 à l’IUFM de Caen en 2012
• Colloque ASI 7 à l’Université PUC de Sao Paulo en 2013
• Colloque ASI 8 à l’ Institut Supérieur Technologique de Radès en 2015
• Colloque ASI 9 à l’Institut Universitaire de Technologie de Belfort-Montbéliard en 2017
• Colloque ASI 10 à l’Institut Universitaire de Technologie de Belfort-Montbéliard en 2019
• Colloque ASI 11 à l’Institut Universitaire de Technologie de Belfort-Montbéliard en 2021