Analyse par enveloppement des données
L'analyse par enveloppement des données (en anglais, data envelopment analysis - abrégée DEA) est une méthode d'analyse comparative non paramétrique de l'efficience. Elle a pour but de comparer des unités de production (ou plus généralement, des unités de prise de décision (en) , en anglais decision making unit abrégé DMU) selon les ressources qu'elles utilisent (les facteurs de productions, ou inputs) et les biens ou services produits produits (outputs). La DEA est basée sur le concept d'ensemble des technologies qui est l'ensemble des plans de productions, c'est-à-dire les outputs pour des facteurs de productions donnés, réalisables technologiquement. Cette méthode d'analyse a été inventée par Abraham Charnes, William W. Cooper et Edward Rhodes.
Historique
La DEA a été inventée par Abraham Charnes, William W. Cooper et Edward Rhodes. Alors doctorant au collège John Heinz III (en) à l'université Carnegie-Mellon sous la supervision de Cooper, Edward Rhodes effectue dans les années 70 une étude sur les résultats du programme fédéral Projet Follow Through, un programme d'éducation pour les élèves provenant de milieux défavorisés ayant été mis en place dans les écoles publiques américaines. Le but de l'étude de Rhodes était de comparer les efficiences relatives des écoles entre celles qui participaient ou non au programme, en les comparant sur base d'inputs utilisés et d'outputs mesurables produits. Cela fut fait grâce à la première forme de DEA, appelée alors « rapport CCR » (des initiales des chercheurs)[1] - [2] - [3].
Principe et formulation mathématique
La DEA a pour but d'étudier les choix de décision de production pris par des unités de prise de décision (en) (en anglais, décision making unit, abrégé DMU)[4]. L'analyse par DEA se fait en deux étapes. Premièrement la détermination de l'ensemble des technologies et secondement le calcul des efficiences par optimisation linéaire.
Le concept d'ensemble des technologies, central à la DEA, est défini comme l'ensemble des points (input X, output Y) tels qu'il est possible, technologiquement, de produire l'output Y avec l'input X. Les unités de production, appelées DMU (pour decision making unit) sont définies par un couple (input, output) correspondant à leur plan de production. Ce couple de points doit appartenir à l'ensemble des technologies. Pour effectuer une DEA, il faudrait connaitre cet ensemble des technologies, cependant, celui-ci est théorique et la plupart du temps inconnu. Il faut donc, en partant d'hypothèses (listées plus bas), déduire l'ensemble des technologies sur bases des données (input,output) des DMU de l'analyse.
Le calcul des efficiences se fait par un calcul d'optimisation. L'efficience est calculé comme le facteur optimal par lequel il faut multiplier les inputs (si l'on recherche l'efficience relative aux inputs) ou bien les outputs (si l'on recherche l'efficience de production pour des inputs donnés) pour que le couple (input, output) se retrouve sur la frontière estimée de l'ensemble des technologies.
Mathématiquement, pour chaque DMU (ici indiquée par k), l'efficience relative aux inputs est définie par
où est l'ensemble des technologies estimé
Ici, l'ensemble dépend des hypothèses prises sur l'ensemble des technologies (voir section suivante).
Formulation des hypothèses
Hypothèses d'estimation de l'ensemble des technologies
L'ensemble des technologies est un concept central en DEA . Il est défini comme l'ensemble formé de tous les couples d'inputs et d'outputs accessibles théoriquement par la technologie actuelle. Lorsque l'on étudiera des entreprises produisant des biens, on parlera de plans de production ; mais la définition d'ensemble des technologies s'applique aussi pour les productions de services. Cependant, cet ensemble n'est, à priori, pas connu. Par exemple, si l'on produit un service et que l'output est le bien-être du consommateur, on ne peut pas savoir quel output maximal est réalisable. On a donc besoin, pour effectuer une DEA, d'estimer l'ensemble des technologies. L'estimation va, sur base d'hypothèses, délimiter la zone des couples d'inputs/outputs réalisables, tout en imposant que tous les points se situent dans l'estimation effectuée (toutes les DMU ont un plan de production accessible, par définition)[1].
Hypothèse de disponibilité libre

L'hypothèse de libre disponibilité (en anglais free disposability hypothesis ou FDH) consiste a supposer que, pour tout couple input/output donné, il y a toujours moyen de produire la même quantité d'output avec plus d'input (en laissant de côté l'input excédentaire non utilisé). De même, pour un input et un output donnés, il y a toujours moyen de produire moins d'output (en laissant de côté l'output excédentaire produit). Enfin, il y a aussi moyen, en mélangeant les deux assertions ci-dessus, de produire moins d'outputs avec plus d'inputs. la FDH dit donc que l'on a toujours la libre disponibilité de faire moins bien qu'un plan de production donné.
Mathématiquement, pour chacune des DMU, dont le couple d'input/output est , l'hypothèse FDH implique que les points produisant moins avec plus, où et appartiennent tous à l'estimation du technology set.
La relation d'ordre prise ici n'est pas totale. En effet, s'il y a par exemple deux variables d'inputs, disons et , il peut arriver que, pour un output donné, une DMU A utilise moins d'input (1) que la DMU B, mais que la DMU B utilise moins d'input (2) que la DMU A. On ne pourra donc pas les comparer : et
On peut graphiquement représenter le technology set résultant de l'hypothèse de disponibilité libre lorsqu'il n'y a qu'un input et qu'un output. L'input est conventionnellement représenté sur l'axe horizontal et l'output sur l'axe vertical. Dans ce cas, le technology set est l'union des zones formées par les « coins inférieurs droits » de chaque plan de production des DMU, c'est-à-dire l'ensemble des points en dessous ou à gauche de chaque plan de production. Sur le graphique ci-contre, le technology set est la zone à droite de la ligne brisée.
Hypothèse de rendements d'échelle variables
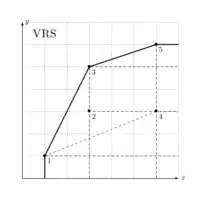
L'hypothèse de rendements d'échelles variables consiste à dire que, si plusieurs DMU ont des plans de productions (couples inputs/outputs) différents, alors une moyenne pondérée de ces plans de productions est un plan de production réalisable. Autrement dit, le point correspondant à cette moyenne pondérée appartient au technology set.
Mathématiquement, si les DMU A et B ont les plans de productions et respectivement, alors tous les points qui sont une moyenne pondérée de ces plans,
appartiennent à l'estimation de l'ensemble des technologies. Cela se généralise pour un nombre fini de points, : si les DMU ont les plans de productions , alors tous les points qui sont une moyenne pondérée de ces plans,
appartiennent à l'estimation de l'ensemble des technologies.
Cela se comprend graphiquement de la manière suivante : pour deux DMU, tous les points qui se situent sur le segment de droite qui les relie sont dans le technology set. La généralisation a plusieurs points signifie que tous les points situé dans le polygone convexe formé par les DMU appartiennent au technology set. La frontière est donc composée d'une ligne brisée. La partie reliant les DMU entre elles provient de l'hypothèsen VRS, l'autre partie de la frontière vient de l'hypothèse de disponibilité libre (qui est toujours assumée). Les points qui se situent à la limite entre ces deux parties s'appellent « points d'ancrage »[5] - [6].
Hypothèses de rendements d'échelle croissant et décroissant
Les hypothèses des rendements d'échelle croissant et décroissant sont une particularisation de l'hypothèse de rendements d'échelle variables. L'hypothèse de rendements d'échelles croissants (en anglais, on l'appelle increasing return to scale - IRS ou bien non-decreasing return to scale - NDRS) suppose que pour tout couple input/output, il y a toujours moyen de produire plus d'output avec le même rapport input/output. Inversement, l'hypothèse de rendement d'échelle de décroissant (decraesing return to scale - DRS ou non-increasing return to scale) stipule qu'il y a toujours moyen de produire moins d'output avec le même rapport input/output.
En termes mathématiques, l'hypothèse des rendements d'échelle croissant se traduit par le fait que pour tout couple input/output de l'ensemble des technologies, le couple est un point valide du technology set. De même, l'hypothèse des rendements d'échelle décroissant se traduit par le fait que pour tout couple input/output de l'ensemble des technologies, le couple est un point valide de l'ensemble des technologies.
Ces deux hypothèses résultent en des technology set convexes.
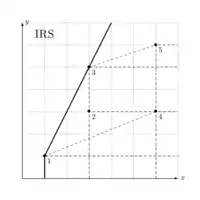 Exemple de rendement d'échelle croissant
Exemple de rendement d'échelle croissant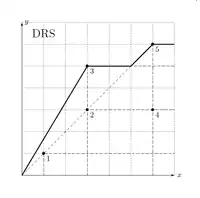 Exemple de rendement d'échelle décroissant
Exemple de rendement d'échelle décroissant
Hypothèse de rendement d'échelle constant
L'hypothèse de rendement d'échelle constant consiste à supposer que pour tout couple d'input output , n'importe quel multiple de ce cette production est réalisable . En termes mathématiques, pour tout couple input/output dans le technology set, tout multiple (avec ) est dans le technology set. Cette hypothèse est donc une généralisation des hypothèses de rendements d'échelle croissant et décroissants et crée donc un technology set convexe.
Exemple comparatif des différentes hypothèses
Supposons que nous voulions comparer 5 entreprises qui produisent chacune un output en utilisant un input . Les couples d'inputs utilisés et output produits sont donnés par la table suivante
| DMU | ||
|---|---|---|
| 1 | 1 | 1 |
| 2 | 3 | 3 |
| 3 | 3 | 5 |
| 4 | 6 | 3 |
| 5 | 6 | 6 |
Selon les hypothèses que l'on choisit pour estimer le technology set, la frontière d'efficience va différer.
 Disponibilité libre
Disponibilité libre Rendements d'échelle variables
Rendements d'échelle variables Rendements d'échelle croissants
Rendements d'échelle croissants Rendements d'échelle décroissants
Rendements d'échelle décroissants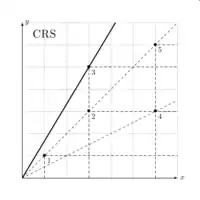 Rendements d'échelle constants
Rendements d'échelle constants
Si nous souhaitons analyse comparative orientée « input » (l'on souhaite donc regarder de combien les inputs peuvent être réduits afin d'être efficient), la DEA consiste juste à calculer le facteur par lequel l'input de chaque DMU doit être multiplié afin que la DMU se retrouve sur la frontière d'efficience.
Par exemple, dans le cas FDH (qui signifie qu'on ne suppose que la libre disponibilité) ci-dessus, les DMU 1,2,3 et 5 sont déjà sur la frontière d'efficience. Leur efficience vaut 1. Quant à la DMU 4, son input doit être multiplié par afin que le point sois sur la frontière d'efficience (et, dans ce cas précis, superposé à la DMU 2).
Dans le cas VRS (qui signifie qu'on suppose la libre disponibilité ainsi que la convexité), les DMU 1,3 et 5 se trouvent sur la frontière ; leur efficience vaut donc 1. La DMU doit avoir son input multiplié par afin d'être sur la frontière, au point . L'efficience de la DMU 2 est donc . Celle de la DMU 4 vaut .
Les efficiences dépendent donc du modèle d'estimation du technology set et donc, de facto, de la façon dont est tracée la frontière. Le tableau ci-dessous donne les efficiences calculées pour les 5 DMU de l'exemple pour les différents modèles.
| DMU | FDH | VRS | IRS | DRS | CRS |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0.6 | 0.6 |
| 2 | 1 | 2/3 | 2/3 | 0.6 | 0.6 |
| 3 | 1 | 1 | 1 | 1 | 1 |
| 4 | 1/2 | 1/3 | 1/3 | 0.3 | 0.3 |
| 5 | 1 | 1 | 0.6 | 1 | 0.6 |
Domaines d'application
La méthode d'analyse de la DEA, consistant à calculer des efficiences relatives de manières non-paramétrique, a été appliqué dans de nombreux domaines, dans des études scientifiques[1]. En effet, un des avantages de la DEA est de pouvoir comparer des entités produisant des biens mais aussi des services (pour lesquels une évaluation purement monétaire de rendement est impossible). Ainsi, dans le domaine de l'éducation, la DEA a été utilisée pour comparer l’efficacité de l'éducation entre les pays nordiques et les autres pays de l'OCDE[7] ou encore mesurer les performances entre universités[8] - [9] ou bien entre départements universitaires d'économie[10]. . Le secteur médical et hospitalier peut aussi être soumis a l'analyse DEA[11] - [12] - [13]. Dans le domaine des entreprises, la satisfaction dans le domaine bancaire[14] ou encore la gestion de la chaine logistique[15] - [16] peuvent être analysée à l'aide de la DEA. Plus folklorique, les résultats olympiques ont été comparés grâce à la DEA[17].
Différences avec la régression linéaire
À première vue, la régression linéaire et l'analyse par enveloppement des données semblent similaires. En effet, ces deux techniques sont des modèles permettant d'analyser des couples input-output et leur relation avec d'autres entreprises ou DMU. Cependant, les différences entre ces deux modèles sont nombreuses[1]. Le tableau suivant recense les principales divergences
| Régression linéaire | Analyse d'enveloppement des données |
|---|---|
| A pour but de calculer une moyenne des pratiques. Les meilleurs et moins bons se compensent. | A pour but de faire ressortir les meilleures pratiques : les meilleurs sont mis en avance par rapport aux autres. |
| Méthode paramétrique. le modèle linéaire est présupposé : les données s'alignent sur une droite avec une certaine erreur. Ces dernières sont indépendantes et identiquement distribuées. Le modèle est nécessaire pour comparer les données. | Modèle non paramétrique : aucune hypothèse sur le comportement des données n'est nécessaire à priori. L'analyse DEA peut se faire en se basant uniquement sur l'hypothèse FDH, qui n'est pas une hypothèse sur la forme (fonctionnelle) des données mais bien sur l'utilisation que l'on en fait. Les données seules sont suffisantes pour pouvoir les comparer entre-elles. |
| L'hypothèse de rendement d'échelle est toujours présente. | L'hypothèse de rendement d'échelle peut être omise. |
| Modèle prédictif. Étant donné un ensemble d'entreprise, une entrée additionnelle aura une valeur définie par la fonction linéaire. | Modèle non prédictif. Le modèle ne peut pas prévoir l'efficience d'une nouvelle DMU étant donnée celle des autres. Il faut recommencer (du moins partiellement) l'analyse. |
| Résultats de l'analyse sujet au modèle choisi. | Résultats de l'analyse entièrement relatifs. Une DMU (ou plus) est toujours entièrement efficiente. |
Notes et références
- Patrick-Yves Badillo et Joseph C. Paradi, La méthode DEA: analyse des performances, Hermes Science Publications, (ISBN 9782746200326, lire en ligne)
- « CCR (ratio) mode » Data Envelopment Analysis: DEAzone.com », sur deazone.com (consulté le )
- (en) Interview de W. Cooper, inventeur de la DEA, « History of Data Envelopment Analysis (DEA) from his Developer Professor William W. Cooper. », (consulté le )
- (en) Encyclopedia of Operations Research and Management Science, Springer, (ISBN 9781461380580, lire en ligne), p. 349
- M.-L. Bougnol et J.H. Dulá, « Anchor points in DEA », European Journal of Operational Research, vol. 192, , p. 668–676 (ISSN 0377-2217, DOI 10.1016/j.ejor.2007.10.034, lire en ligne, consulté le )
- R. Allen et E. Thanassoulis, « Improving envelopment in data envelopment analysis », European Journal of Operational Research, dEA and its uses in different countries, vol. 154, , p. 363–379 (DOI 10.1016/S0377-2217(03)00175-9, lire en ligne, consulté le )
- Peter Bogetoft, Eskil Heinesen et Torben Tranæs, « The efficiency of educational production: A comparison of the Nordic countries with other OECD countries », Economic Modelling, vol. 50, , p. 310–321 (DOI 10.1016/j.econmod.2015.06.025, lire en ligne, consulté le )
- Melville McMillan et Debasish Datta, « The Relative Efficiencies of Canadian Universities: A DEA Perspective », Canadian Public Policy, vol. 24, , p. 485–511 (lire en ligne, consulté le )
- Marie-Laure Bougnol et José H. Dulá, « Validating DEA as a ranking tool: An application of DEA to assess performance in higher education », Annals of Operations Research, vol. 145, , p. 339–365 (ISSN 0254-5330, DOI 10.1007/s10479-006-0039-2, lire en ligne, consulté le )
- (en) Jill Johnes et Geraint Johnes, « Measuring the Research Performance of UK Economics Departments: An Application of Data Envelopment Analysis », Oxford Economic Papers, vol. 45, , p. 332-347 (ISSN 1464-3812, lire en ligne, consulté le )
- Diego Prior, « Efficiency and total quality management in health care organizations: A dynamic frontier approach », Annals of Operations Research, vol. 145, , p. 281–299 (ISSN 0254-5330, DOI 10.1007/s10479-006-0035-6, lire en ligne, consulté le )
- Juan Du, Justin Wang, Yao Chen et Shin-Yi Chou, « Incorporating health outcomes in Pennsylvania hospital efficiency: an additive super-efficiency DEA approach », Annals of Operations Research, vol. 221, , p. 161–172 (ISSN 0254-5330, DOI 10.1007/s10479-011-0838-y, lire en ligne, consulté le )
- Pyb Mané, « Analyse de l'efficience des hôpitaux du Sénégal : application de la méthode d'enveloppement des données », Pratiques et Organisation des Soins, vol. 43, no 4, , p. 277–283 (ISSN 1952-9201, lire en ligne, consulté le )
- E. Grigoroudis, E. Tsitsiridi et C. Zopounidis, « Linking customer satisfaction, employee appraisal, and business performance: an evaluation methodology in the banking sector », Annals of Operations Research, vol. 205, , p. 5–27 (ISSN 0254-5330, DOI 10.1007/s10479-012-1206-2, lire en ligne, consulté le )
- Zhongbao Zhou, Mei Wang, Hui Ding et Chaoqun Ma, « Further study of production possibility set and performance evaluation model in supply chain DEA », Annals of Operations Research, vol. 206, , p. 585–592 (ISSN 0254-5330, DOI 10.1007/s10479-013-1365-9, lire en ligne, consulté le )
- Yao Chen, Liang Liang et Feng Yang, « A DEA game model approach to supply chain efficiency », Annals of Operations Research, vol. 145, , p. 5–13 (ISSN 0254-5330, DOI 10.1007/s10479-006-0022-y, lire en ligne, consulté le )
- Xiyang Lei, Yongjun Li, Qiwei Xie et Liang Liang, « Measuring Olympics achievements based on a parallel DEA approach », Annals of Operations Research, vol. 226, , p. 379–396 (ISSN 0254-5330, DOI 10.1007/s10479-014-1708-1, lire en ligne, consulté le )














![{\displaystyle (\lambda x_{A}+(1-\lambda )x_{B},\lambda y_{A}+(1-\lambda )y_{B}),{\text{ avec }}\lambda \in [0,1]}](https://img.franco.wiki/i/14f015e238ae341ba32fac54090819ab58df5be9.svg)

















