Algorithme de recherche de sous-chaîne

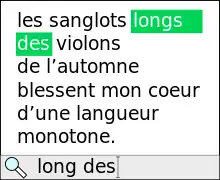
L'algorithme naïf consiste consiste à faire glisser le motif le long du texte[2]. A début, le motif se trouve aligné avec le début du texte. Par exemple si l'on cherche la chaîne longs des dans le texte les sanglots longs des violons de l'automne blessent mon cœur d'une langueur monotone on considère l'alignement suivant :

les sanglots longs des violons de l'automne blessent mon cœur d'une langueur monotone.
longs des

On compare caractère après caractère le motif et le texte. Le première caractère est l. Mais le deuxième caractère est différent. On fait alors glisser le motif d'une case vers la droite.

les sanglots longs des violons de l'automne blessent mon cœur d'une langueur monotone.
 longs des

On compare caractère après caractère le motif et le texte à partir du second caractères. Le caractère e et l sont différents. On continue donc à glisser le motif.

les sanglots longs des violons de l'automne blessent mon cœur d'une langueur monotone.
  longs des   
   longs des  
    longs des
     longs des
      longs des
       longs des
        longs des
         longs des
          longs des
           longs des
            longs des

Au prochain glissement, l'alignement coïncide :

les sanglots longs des violons de l'automne blessent mon cœur d'une langueur monotone.
             longs des

Si tous les caractères correspondent, comme c'est le cas là, on retourne la position du premier caractère de la chaîne trouvée dans la chaîne initiale. Si jamais nous avons glissé le motif jusqu'à la fin du texte, mais que l'alignement ne coïncidait jamais, alors l'algorithme échoue. Dans certaines implémentations, l'algorithme retourne -1.

On note |m| le nombre de caractères dans m. On suppose que les indices dans les chaînes de caractères commencent à 0. Voici le pseudo-code de l'algorithme naïf :

entrée : un motif m, un texte
sortie : la position du motif m dans le texte; ou -1 si le motif ne s'y trouve pas
fonction rechercherNaïve(m, texte)
       pour tout i = 0 à |texte| - |m| - 1
              si m = texte[i, i+|m|-1] alors
                      renvoie i
       renvoie -1

Cependant, la complexité algorithmique étant Θ(|texte|*|m|). Plus précisément, l'algorithme effectue |m|(|texte| - |m| 1) comparaisons dans le pire cas[2]. Ce pire cas arrive par exemple si l'on cherche le motif aa..ab dans un texte aa..aa, comme :

texte :            aaaaaaaaaaaaaaaaaaaaaaa
motif à chercher : aaaaab

En effet, à chaque position de la fenêtre glissante du motif, on réalise |m| comparaisons de caractères et il y a (|texte| - |m| - 1) positions différentes. Dans le meilleur des cas[2], on ne fait qu'une seule comparaison pour chaque position de fenêtre et dans ce cas on fait |texte| - |m| - 1 comparaisons.

Toutefois, pour un algorithme de plus de deux lettres, et si la distribution sur les lettres est indépendante et uniforme, alors le nombre moyen de comparaisons de caractères pour rechercher un motif avec l'algorithme naïf dans un texte est au plus 2|texte| (voir Proposition 1.1 dans [1]).

Article détaillé - Algorithme de Boyer-Moore

Article détaillé - Algorithme de Boyer-Moore-Horspool

Article détaillé - Algorithme de Raita

Dans l'algorithme de Boyer-Moore[3] la comparaison m = texte[i, i+|m|-1] s'effectue en faisant des comparaisons de caractères de droite vers la gauche (alors qu'a priori, dans l'algorithme naïf, on effectue des comparaisons de gauche à droite). Puis on augmente la valeur de i de la manière suivante. Soit j l'indice où il y a la première différence, c'està-dire tel que j le plus grand avec m[j] différent de t[i+j]. On augmente alors i de j - k, où k est le grand entier tel que avec k dans [0, ... j-1] et m[k] = t[i+j] si un tel k existe. S'il n'y a pas de tel k, alors on augmente k de j+1.

Considérons l'exemple où l'on cherche le motif m qui estabracadabra. Supposons que l'on teste l'égalité entre le motif m et texte[i, i+|m|-1]. Pour l'instant, nous avons constaté égalité des 5 dernières lettres de m et texte[i, i+10], à savoir dabra. Par contre, on constate une différence dans la 6e lettre en partant de la fin : il y a un b dans le texte alors qu'il y a un a dans le motif.

                                  i
texte :                           ?????bdabra????
motif :                           abracadabra                      

L'algorithme naïf aurait décaler le motif juste d'une case (incrémenter i de un). En image :

                                   i
texte :                           ?????bdabra????
motif :                            abracadabra               (décalage de 1)                

Regardons dans les incrémentations suivantes, la prochaine qui vient placer un b sous le b du texte :

texte :                           ?????bdabra????
                                   abracadabra               (décalage de 1)
                                    abracadabra              (décalage de 2)
                                     abracadabra             (décalage de 3)
                                      abracadabra            (décalage de 4)

L'algorithme de Boyer-Moore effectue ce décalage de 4 immédiatement, en ayant effectué un prétraitement sur le motif.

Article détaillé - Algorithme de Knuth-Morris-Pratt

Article détaillé - Algorithme de Baeza-Yates-Gonnet

Article détaillé - Algorithme Z

Article détaillé - Algorithme de Rabin-Karp.

Article détaillé - Algorithme d'Aho-Corasick.

Il existe beaucoup de formats de textes dans lesquels chercher, et en conséquence tous les algorithmes sont susceptibles de connaître de fortes variations suivant le texte fourni.

Par exemple, la taille du texte peut varier de la simple ligne à la concaténation de milliers de livres. L'encodage du texte peut également avoir une influence dramatique sur la performance d'un algorithme. Notamment, des alphabets de type ADN, ASCII ou Unicode peuvent exclure d'office l'utilisation d'un algorithme particulier.

Les algorithmes sus-cités sont académiques. En pratique ils sont fortement adaptés pour répondre aux besoins sur le terrain.

Certaines bibliothèques combinent de multiples algorithmes pour rester dans le meilleur cas de résolution possible. Par exemple stringlib/fastsearch[4] en Python utilise la force brute pour P de longueur 1 et une combinaison de Boyer-Moore-Horspool et Sunday et des filtres de Bloom pour remplacer la table de saut.

Certains programmes tel grep offrent une myriade d'optimisations[5] et sacrifient leur worst-case au best-case[6], en pariant sur le fait que P et T ont une faible probabilité d'engendrer un cas pathologique.

Enfin, les processeurs modernes offrent des jeux d'instructions SIMD particulièrement efficaces tel SSE. Certaines implémentations de libc strstr utilisent ces instructions pour accélérer la recherche.