Algorithme de Green et Sibson

Construction du diagramme de Voronoï selon l'algorithme de Green et Sibson.

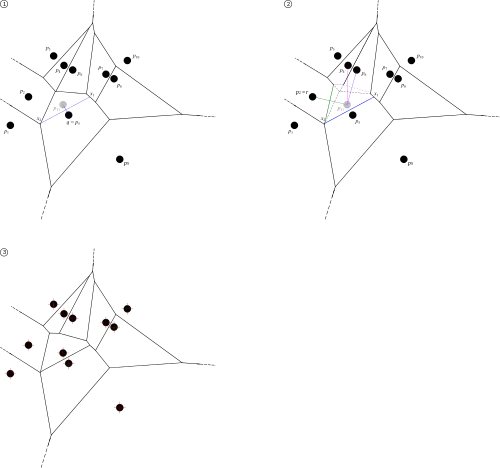
L'algorithme est incrémental[1]. On ajoute les points les uns après les autres, en mettant à jour le diagramme. l'idée est que l'ajout d'un point ne va modifier le diagramme que localement[1].

Soit S = {p₁, p₂, …, p_n}. Supposons que le diagramme est construit pour les k premiers germes ; on ajoute le germe k + 1. Comme le diagramme de Voronoï est une partition du plan, le point p_{k + 1} est nécessairement dans (au moins) une région du diagramme de Voronoï des k premiers points ; soit q le germe de cette région.

On considère la médiatrice de [p_{k + 1}q]. Comme la région est convexe, cette médiatrice a exactement deux points d'intersection avec les parois de la cellule. Soient x₁ et x₂ ces points d'intersection, le triangle qx₁x₂ étant orienté dans le sens direct. Le segment [x₁x₂] réduit la région Vor_{{p1, …, pk}}(q), ce qui nous donne directement Vor_{{p1, …, pk + 1}}(q).

Le point x₂ est sur la paroi d'une cellule, il appartient donc également à une cellule générée par un germe r. On considère alors la médiatrice de [p_{k + 1}r], et ainsi de suite jusqu'à revenir au point x₁. On trace ainsi une suite de parois qui font le tour du point p_{k + 1}, et qui définissent de nouvelles cellules.

L'algorithme de Green et Sibson est de complexité en temps O(n²)[1].

Cet algorithme a été décrit par Peter Green et Robin Sibson en 1978[2].

D'autres algorithmes sont plus rapides, de complexité ${\displaystyle O(n\log n)}$, comme l'algorithme de Fortune et l'algorithme de Shamos et Hoey. Le premier est un algorithme de type sweep line et le second est de type diviser pour régner[1].

• Cet article est partiellement ou en totalité issu de l'article intitulé « Diagramme de Voronoï » (voir la liste des auteurs).