Équation de Landau-Lifshitz-Gilbert

Les termes de l'équation de Landau-Lifshitz-Gilbert : précession (en rouge) et amortissement (en bleu). La trajectoire de l'aimantation (spirale de pointillés) est dessinée en supposant pour simplifier que le champ effectif H_eff est constant.

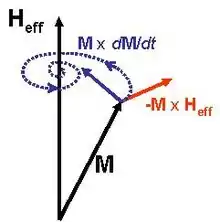
Dans un matériau ferromagnétique, l'aimantation M peut varier dans l'espace mais son amplitude est égale en tout point à l'aimantation à saturation M_s. L'équation de Landau–Lifshitz–Gilbert prédit la rotation de l'aimantation en réponse à des moments appliqués. L'équation antérieure, mais équivalente (Laudau-Lifshitz) a été introduite par Landau et Lifshitz[3] - [4] - [2] :

${\displaystyle {\frac {d\mathbf {M} }{dt}}=-\gamma \mathbf {M} \times \mathbf {H_{\mathrm {eff} }} -\lambda \mathbf {M} \times \left(\mathbf {M} \times \mathbf {H_{\mathrm {eff} }} \right)}$

où γ est le rapport gyromagnétique de l'électron et λ est un paramètre phénoménologique d'amortissement, souvent remplacé par

${\displaystyle \lambda =\alpha {\frac {\gamma }{M_{\mathrm {s} }}},}$

où α est une constante sans dimension appelée facteur d'amortissement. Le champ effectif H_eff est une combinaison du champ magnétique externe, du champ de désaimantation, d'effets quantiques et d'éventuelles autres contributions (magnétostriction, anisotropie magnétique...). Afin de résoudre cette équation, il est nécessaire d'y ajouter d'autres équations permettant de déterminer le champ de désaimantation, qui est globalement généré par la distribution d'aimantation du milieu considéré.

Il convient de noter que cette équation répond aux attentes sur le comportement des moments magnétiques : conservation de l'amplitude du moment, et précession avec alignement progressif avec le champ effectif. De nombreux auteurs ont obtenu cette équation de manière indépendante[1].

En 1955, Gilbert proposa de remplacer le terme d'amortissement dans l'équation de Landau-Lishitz par un terme qui dépend de la dérivée de l'aimantation par rapport au temps :

${\displaystyle {\frac {d\mathbf {M} }{dt}}=-\gamma \left(\mathbf {M} \times \mathbf {H} _{\mathrm {eff} }-\eta \mathbf {M} \times {\frac {d\mathbf {M} }{dt}}\right)}$

C'est l'équation de Landau-Lifshitz-Gilbert (LLG), où η est le paramètre d'amortissement, qui est caractéristique du matériau. On peut retrouver l'équation de Landau-Lifshitz[4] :

${\displaystyle {\frac {d\mathbf {M} }{dt}}=-\gamma '\mathbf {M} \times \mathbf {H} _{\mathrm {eff} }-\lambda \mathbf {M} \times (\mathbf {M} \times \mathbf {H} _{\mathrm {eff} })}$

où

${\displaystyle \gamma '={\frac {\gamma }{1+\gamma ^{2}\eta ^{2}M_{s}^{2}}}\qquad {\text{et}}\qquad \lambda ={\frac {\gamma \eta }{1+\gamma ^{2}\eta ^{2}M_{s}^{2}}}.}$

Sous cette forme de l'équation de Landau-Lifshitz, le facteur γ' du terme de précession dépend du facteur d'amortissement. Cela rend mieux compte du comportement des milieux ferromagnétiques réels lorsque l'amortissement est important[5].

En 1996, Slonczewski (en) a étendu le modèle pour rendre compte du phénomène de transfert de spin, c'est-à-dire le moment induit sur l'aimantation par un courant polarisé en spin traversant le milieu. On utilise souvent le moment unitaire défini par ${\displaystyle {\hat {m}}={\vec {M}}/M_{S}}$:

${\displaystyle {\dot {\hat {m}}}=-\gamma {\hat {m}}\times {\vec {H}}_{\mathrm {eff} }+\alpha {\hat {m}}\times {\dot {\hat {m}}}+\tau _{\parallel }{\frac {{\hat {m}}\times ({\hat {x}}'\times {\hat {m}})}{\left|{\hat {x}}'\times {\hat {m}}\right|}}+\tau _{\perp }{\frac {{\hat {x}}'\times {\hat {m}}}{\left|{\hat {x}}'\times {\hat {m}}\right|}}}$

où ${\displaystyle \alpha }$ est le paramètre d'amortissement sans unité, ${\displaystyle \tau _{\perp }}$ et ${\displaystyle \tau _{\parallel }}$ sont les moments perpendiculaires et parallèles, et ${\displaystyle {\hat {x}}'}$ est le vecteur unitaire représentant la direction de polarisation du courant.

• William Fuller Brown, Micromagnetics, Robert E. Krieger Publishing Co., 1978 (1^re éd. Originally published in 1963) (ISBN 0-88275-665-6)
• (en) Sōshin Chikazumi, Physics of Ferromagnetism, Oxford, Clarendon Press, 1997, 655 p. (ISBN 0-19-851776-9)

• (en) Amikam Aharoni, Introduction to the Theory of Ferromagnetism, Oxford, Clarendon Press, 1996, 315 p. (ISBN 0-19-851791-2)