Écoulements torrentiel et fluvial
L'écoulement fluvial et l'écoulement torrentiel sont les deux grands régimes d'écoulement que l'on dénote dans la nature. Ils traduisent notamment l'équilibre de l'écoulement dans un canal que ce soit une rivière, un cours d'eau ou encore un conduit fermé. Ce type d'écoulement est relativement complexe, car il présente une surface libre (zone de contact air/fluide). La surface du fluide n'est pas contrainte par une surface (comme c'est le cas dans un tuyau d'arrosage par exemple) mais uniquement par la pression atmosphérique. Ainsi, cette surface peut se déformer (courbure de la surface, augmentation ou diminution du tirant d'eau, etc.) en fonction des caractéristiques du canal et des contraintes extérieures. C'est pourquoi l'écoulement peut varier dans le temps et dans l'espace en fonction du débit, de la pente du canal, de sa section et de la présence ou non d'obstacle dans le lit du canal. Dans ce genre de configuration, l'écoulement est en pratique majoritairement gouverné par la pente du canal et moins par la différence de charge (comme c'est le cas avec la pression dans le cas d'un écoulement de Poiseuille).


Caractéristique d'un canal et de l'écoulement
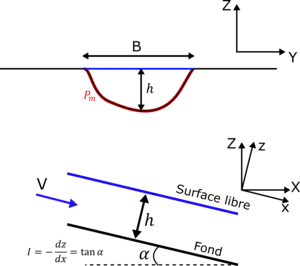
L'écoulement au sein d'un canal, d'une rivière, d'un fleuve ou encore d'une canalisation peut être caractérisé par un certain nombre de grandeurs physiques[1] - [2] - [3] - [4] définies ci-dessous:
- La section du canal: géométrie du canal dans l'axe perpendiculaire au sens de l'écoulement
- Le tirant d'eau ou hauteur d'eau : distance entre le point le plus bas de la section et la surface libre
- La section mouillée : limitation de la section du canal par les parois et la surface libre
- La largeur au miroir : largeur de la section mouillée au niveau de la surface libre
- La hauteur du fond
- La hauteur de la surface libre
- Le débit
- La vitesse moyenne de l'écoulement
- La pente du canal
- Le périmètre mouillé : périmètre de la section mouillée ayant un contact avec les parois
- Le rayon hydraulique
Le périmètre mouillé et le rayon hydraulique sont des grandeurs calculables[1] - [2] en fonction de la géométrie du canal dont certains exemples sont mis en évidence dans le calcul du diamètre hydraulique et brièvement rappelé ci-dessous.
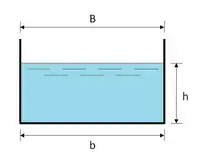 Rectangle |
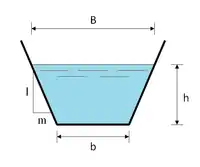 Trapèze |
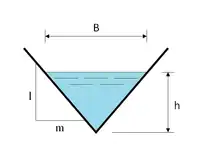 Triangle |
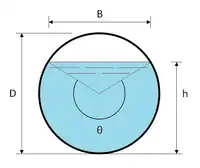 Cercle | ||
|---|---|---|---|---|---|
| Largeur, | ou | ||||
| Surface, | |||||
| Périmètre mouillé, |
|||||
| Rayon hydraulique, |
Classification du type d'écoulement
Afin de déterminer si un écoulement est plutôt fluvial ou torrentiel, on utilise généralement le nombre de Froude[1] - [2] - [3] - [4]. Il est défini comme le rapport entre la vitesse de l'écoulement et la vitesse des ondes de surface (aussi appelée ondes gravitationnelles).
où V est la vitesse, g l'accélération de pesanteur et h la hauteur d'eau.
Si l'on considère que l'on se place dans le cas d'un écoulement à vitesse constante, on observe que le nombre de Froude est uniquement dépendant de la hauteur de l'écoulement. On peut alors définir la hauteur critique de cet écoulement comme la hauteur pour laquelle les ondes de surface se propagent à la même célérité que l'écoulement [1] - [2] - [3]. Nous verrons par la suite que la hauteur d'eau est fonction de la pente du canal. On peut ainsi définir une pente critique pour laquelle . On peut alors mettre en évidence 3 grands régimes d'écoulement.
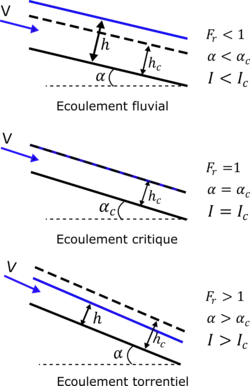
Régime fluvial (Cas subcritique)
Le régime fluvial est caractérisé par un nombre de Froude . Ainsi, la célérité des ondes de surface est supérieure à la vitesse de l'écoulement du fluide. Ceci se traduit par une hauteur d'eau importante et supérieure à la hauteur d'eau critique de l'écoulement (). La pente de l'écoulement est quant à elle inférieure à la pente critique de l'écoulement ().
Régime critique
Le régime critique est caractérisé par un nombre de Froude . Ainsi, la célérité des ondes de surface est égale à la vitesse de l'écoulement du fluide. Ceci se traduit par une hauteur d'eau égale à la hauteur d'eau critique de l'écoulement (). La pente de l'écoulement est donc égale à la pente critique de l'écoulement ().
Régime torrentiel (Cas supercritique)
Le régime torrentiel est caractérisé par un nombre de Froude . Ainsi, la célérité des ondes de surface est inférieure à la vitesse de l'écoulement du fluide. Ceci se traduit par une hauteur d'eau faible et inférieur à la hauteur d'eau critique de l'écoulement (). La pente de l'écoulement est quant à elle supérieure à la pente critique de l'écoulement ().
Précision sur le caractère turbulent de l'écoulement
Le nombre de Reynolds est utilisé en plus du nombre de Froude afin de caractériser plus finement le type d'écoulement, en particulier son caractère turbulent[1].
où correspond à la viscosité cinématique du fluide. Ainsi, on peut préciser:
- , écoulement fluvial et laminaire
- , écoulement fluvial et turbulent
- , écoulement torrentiel et laminaire
- , écoulement torrentiel et turbulent
Transition entre les régimes

On observe une transition du régime fluvial vers un régime torrentiel dans différentes configurations. Si la pente du canal augmente et dépasse la pente critique de l'écoulement, la hauteur d'eau deviendra plus faible que la hauteur d'eau critique[1] - [2] - [3]. On sera alors en régime torrentiel. Si la pente reste constante, il est également possible d'observer une transition du régime fluvial vers le régime torrentiel. Cette transition apparaît par exemple lorsque la section du canal diminue ou que des obstacles se trouvent au fond. En effet, la section mouillée étant plus faible et le débit volumique constant, la vitesse de l'écoulement augmente. Si la vitesse augmente suffisamment, il est possible d'obtenir , et donc de se retrouver dans une configuration d'écoulement torrentiel.
Il est également possible d'observer des transitions du régime torrentiel vers le régime fluvial. Ceci se produit pour des variations inverses de celles décrites précédemment. Cette transition s'accompagne également d'un ressaut hydraulique et d'une perte d'énergie.

Définition de la charge hydraulique
Charge en un point
La charge hydraulique correspond en réalité à l’énergie par unité de poids en un point. Cette quantité peut être décrite en termes de hauteur de colonne d'eau comme la somme de l'énergie potentielle, de l'énergie de pression et de l'énergie cinétique. Pour l'exprimer, on se sert souvent du théorème de Bernouilli. Dans notre cas, la charge au point M s'exprime comme suit[1] - [2] - [3] - [4]:
Charge moyenne
La charge moyenne revient à calculer la moyenne de la charge dans la section mouillée[1]. On l'écrit:
On obtient après calcul:
Charge spécifique
La charge spécifique revient à calculer la charge par rapport au fond du canal et non par rapport à l'origine du repère[1]. On la définit donc comme:
Grandeurs caractéristiques de l'écoulement
Régime établi
On parle de régime établi d'un écoulement lorsque ce dernier possède des caractéristiques constantes dans l'espace et au cours du temps. Ainsi, le débit, la vitesse de l'écoulement, la hauteur d'eau et la surface mouillée sont des constantes.
Profondeur de l'écoulement
L'application du théorème de Bernoulli avec perte de charge sur une ligne de courant entre deux points au niveau de la surface libre revient à écrire:
Or, toutes les grandeurs sont constantes. Il reste seulement:
avec
on obtient donc:
où I est la pente de l'écoulement. C'est l'équation du régime établi (ou uniforme).
Or, cette perte de charge est directement liée aux frottements fluides. On note le coefficient de friction comme:
avec la force de friction. Ce dernier en peut être réécrit en appliquant le principe fondamental de la dynamique sur une particule de fluide comme . On retombe sur la formule de Chezy [1] - [2] - [3] - [4] reliant la pente de l'écoulement à sa vitesse:
Cette formule a été par la suite complétée avec la formule de Manning-Strickler [1] - [2] - [3] - [4] pour laquelle où ks est un coefficient. Ce qui donne:
Comme nous sommes en régime uniforme I=J. On peut donc réécrire:
où et sont des fonctions de la hauteur d'eau . La résolution de cette équation donne la hauteur de l'écoulement.
Profondeur critique de l'écoulement
La profondeur critique de l'écoulement peut s'obtenir de deux manières différentes soit en minimisant la charge hydraulique, soit en maximisant le débit volumique[1] - [3].
- Méthode 1: Minimisation de la charge:
or et on note
on obtient donc:
La résolution de cette équation donne la valeur de la hauteur d'eau critique.
- Méthode 2: Maximisation du débit
On a ce qui permet d'écrire le débit . La maximisation donne:
Ceci nous amène donc à obtenir la même équation que précédemment sous une forme légèrement différente.
Caractérisation de l'écoulement
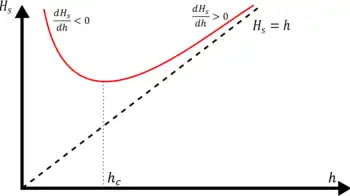
Posons nous avons
Dans le cas d'un écoulement dans un canal donc .
- Si c'est le régime critique
- Si c'est le régime fluvial
- Si c'est le régime torrentiel
Pente critique de l'écoulement
La valeur de la pente critique [1] - [3] est obtenue lorsque et donc ce qui nous donne:
or en utilisant la formule de Manning-Strickler on obtient:
La résolution de cette équation nous donne la pente critique.
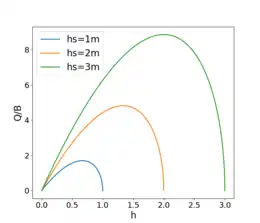
Cas d'un canal rectangulaire à faible pente
Dans le cas d'un canal rectangulaire à faible pente, nous avons et .
Le débit volumique s'écrit:
La formule donnant la hauteur d'eau de l'écoulement s'écrit en appliquant la formule de la méthode 2 de la section profondeur critique de l'écoulement, on obtient:
ce qui nous donne une profondeur critique:
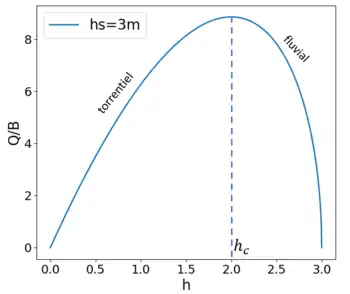
On voit ici que pour un même débit, deux hauteurs d'eau sont possibles. Une faible hauteur d'eau implique une vitesse élevée et donc un régime torrentiel. Une hauteur d'eau élevée implique une faible vitesse et donc un écoulement fluvial.
Ecoulement graduellement varié
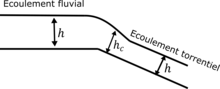
Un écoulement graduellement varié permet de caractériser l'écoulement lors d'un changement de pente qui va donc entraîner le passage d'un régime fluvial au régime torrentiel ou inversement [1] - [3].
On sait que l'on a:
ce qui nous donne
or on sait que l'on a:
La division des deux équations nous donne:
Cette équation permet de caractériser l'évolution de la profondeur de l'eau en fonction de x.
Ecoulement rapidement varié
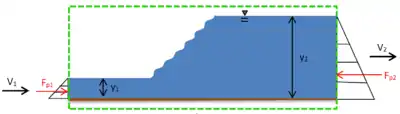
Le ressaut hydraulique est une surélévation brutale de la surface libre d'un écoulement permanent. Ce phénomène apparaît notamment lors d'un passage du régime torrentiel au régime fluvial. Il s'accompagne d'une chute brutale d'énergie et d'une baisse de la vitesse d'écoulement.
On appelle et les profondeurs conjuguées du ressaut [1] - [3]. Dans ce genre de configuration, le théorème de Bernoulli n'est plus applicable, d'une part car nous ne sommes plus en régime permanent et d'autre part, car la perte de charge n'est pas connue. Ainsi, pour déterminer la relation entre ces hauteurs, on utilise le théorème de la quantité de mouvement[1] - [3]:
avec le débit massique. En négligeant les forces de frottement et de pesanteur, nous avons dans le cas d'un canal rectangulaire:
avec et on note . On obtient la relation suivante:
La résolution de cette équation nous donne les deux relations suivantes[1] - [3]:
En moyenne, la formule empirique qui permet de déterminer la longueur sur laquelle s'étend un ressaut est la suivante[1]:
La perte de charge causée par le ressaut est donnée par la formule suivante[1]:
Exemple d'un écoulement naturel
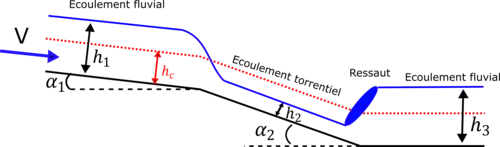
Comportement de la hauteur d'eau avec une variation de largeur du canal : exemple d'un canal rectangulaire.
Supposons que la largeur du fleuve diminue et passe de la largeur B à la largeur avec .
On sait que en prenant le logarithme, on obtient:
Le débit restant étant constant, la différentielle de cette équation donne:
sachant de , on obtient:
Ainsi si alors . Cela signifie que si initialement l'écoulement est fluvial, un rétrécissement du canal entraine une diminution de la hauteur d'eau. Inversement, si alors , ce qui signifie qu'un écoulement torrentiel a tendance à voir sa hauteur d'eau augmenter lorsque le canal se rétrécit.
Voir aussi
Références
- (en) ova, « ECOULEMENTS A SURFACE LIBRE », sur SlideServe,
- SAOULI Abdallah, PROBLEMATIQUE DU RISQUE INONDATION EN MILIEU URBAIN CAS DE LA VILLE D’EL-BAYADH,
- Peter Steffler, « Hydraulics of Open Channel Flow », Journal of Hydraulic Engineering, vol. 125, no 11, , p. 1225–1226 (ISSN 0733-9429 et 1943-7900, DOI 10.1061/(asce)0733-9429(1999)125:11(1225), lire en ligne, consulté le )
- Chow, Ven Te., Open-channel hydraulics, McGraw-Hill, (ISBN 0-07-010776-9 et 978-0-07-010776-2, OCLC 802535085, lire en ligne)
Sources et bibliographie
- Noui, Abderrahmane & Abdellah, Saouli. (2019). PROBLÉMATIQUE DU RISQUE INONDATION EN MILIEU URBAIN ; CAS DE l'AGGLOMÉRATION D'ELBAYADH.
- Anonyme, 1954. Handbook of Channel Design for Soil and Water Conservation. United State Department of Agriculture, Soil Conservation Service. SCS--TP--61.
- https://www.slideserve.com/ova/ecoulements-a-surface-libre
- Chow, Ven Te, 1959. Open--Channel Hydraulics. McGraw--Hill, Toronto.
- French, R. H. 1999. Hydraulics of Open Channel Flow. Dans : Mays, L. W. (éd.). 1999. Hydraulic Design Handbook. Mc Graw Hill, New York.
- Schwab, G.O., R.K. Frevert, T.W. Edminster et K.K. Barnes, 1966. Soil and Water Conservation Engineering.
- John Wiley and Sons, New York. Simon, A.L., 1976. Practical Hydraulics. John Wiley and Sons, Toronto.




























![{\displaystyle {\frac {1}{4}}\left[1-{\frac {\sin \theta }{\theta }}\right]D}](https://img.franco.wiki/i/8edbced6d2b2aabafd894e05f762f8a314209ea1.svg)




















































































