Écoulement de Hiemenz
L'écoulement de Hiemenz est un écoulement potentiel de point d'arrêt en symétrie plane dont la solution est analytique au sens où elle se ramène à la résolution d'une simple équation différentielle. Il a été décrit par Karl Hiemenz dans sa thèse à l'université de Göttingen en 1911[1] et a été étendu au cas de la symétrie de révolution par Fritz Homann en 1936[2].
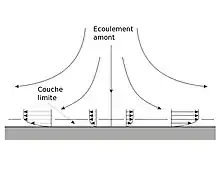
Solution de Hiemenz
Le problème posé est celui d'un écoulement irrotationnel impactant un cylindre perpendiculairement à celui-ci. Le potentiel est , étant l'axe portant l'écoulement amont[3]. Les composantes de la vitesse dans le milieu amont sont :
Si est la pression au point d'arrêt, la pression en tout point est donnée par la conservation de quantité de mouvement :
Au voisinage de la paroi il apparaît une couche limite et la solution générale est recherchée sous la forme suivante :
Ces équations satisfont par construction à l'équation de continuité. La conservation de quantité de mouvement conduit à :
où υ est la viscosité cinématique.
Les conditions aux limites sont :
La première équation est indépendante et peut être transformée en posant :
Elle devient :
En posant :
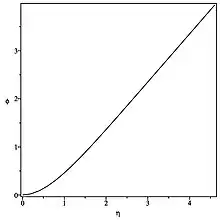
Elle devient l'équation adimensionée :
avec les conditions aux limites :
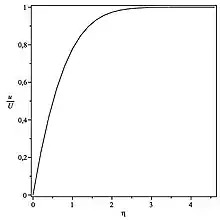
La vitesse relative parallèle à la paroi (dans la « couche limite ») est indépendante de x :
L'accélération pariétale est .
Si l'on prend pour définition de l'épaisseur de couche limite , l'épaisseur de celle-ci (voir courbe) est donnée par .
Généralisations
La méthode a été généralisée à un point d'arrêt axisymétrique[3], à un jet en incidence et à des parois en mouvement, par exemple un cylindre en rotation.
Références
- (de) Karl Hiemenz, Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder,
- (de) Fritz Homann, « Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel », Zamm, vol. 16, no 3, , p. 153–164
- (en) Hermann Schlichting, Boundary Layer Theory, McGraw Hill, (ISBN 3662570955, lire en ligne)


















